δ
(valor exacte) |
δ
(valor) |
Nom |
Representació |
Observacions
|
 |
0,4498? |
Bifurcació de la corba logística |
![]() |
El atractor de Feigenbaum (entre les fletxes) és el conjunt de punts generat per successives iteracions de la funció logística per al valor del paràmetre crític  , on el període de duplicament és infinit. Aquesta dimensió és la mateixa per a qualsevol funció diferenciable i unimodal.[1] , on el període de duplicament és infinit. Aquesta dimensió és la mateixa per a qualsevol funció diferenciable i unimodal.[1]
|
 |
0,6309 |
Conjunt de Cantor |
 |
Es construeix eliminant l'interval central en cada iteració. És un conjunt dens enlloc i no numerable.
|
 |
1 |
Conjunt de Smith-Volterra-Cantor |
 |
Es construeix eliminant l'interval central de longitud  de cadascun del intervals en cada iteració. És dens enlloc i amb mesura de Lebesgue de ½. de cadascun del intervals en cada iteració. És dens enlloc i amb mesura de Lebesgue de ½.
|
| Calculat |
1.0812 |
Conjunt de Julia z² + 1/4 |
 |
Conjunt de Julia per a c = 1/4.
|
 |
1.12915 |
Contorn de l'illa de Gosper |
 |
|
| Calculat (compte de caixes) |
1.2 |
Conjunt de Julia Dendrita |
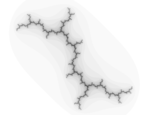 |
Conjunt de Julia per als paràmetres: Real = 0 i Imaginari = 1.
|
 |
1,2083 |
Fractal de Fibonacci (60°) |
 |
Construcció a partir de la paraula de Fibonacci.
|
 |
1.2619 |
Corba de Koch |
 |
Tres corbes de Koch formen el floc de neu de Koch (o el antifloc de neu de Koch).
|
 |
1.2619 |
3-Antifloc de neu de Koch |
 |
Antifloc de neu de Koch format per 3 corbes de Koch.
|
 |
1.2619 |
frontera de la corba del terdrac |
 |
Sistema L: anàloga a la corba del drac amb angle de 30°.
|
 |
1.2619 |
Pols de Cantor bidimensional |
 |
Pols de Cantor en 2D.[2]
|
| Calculat |
1.2683 |
Conjunt de Julia z²-1 |
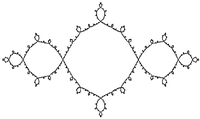 |
Conjunt de Julia per a c = -1.[3]
|
|
1,3057 |
Circumferència d'Apol·loni |
 |
vegeu [4]
|
| Calculadt |
1.3934 |
Conill de Douady |
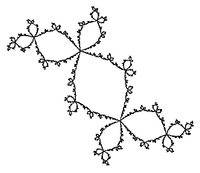 |
Conjunt de Julia per a c = -0,123 + 0,745i.[5]
|
 |
1.4649 |
Fractal de Vicsek |
 |
Es construeix per substitució iterativa d'un quadrat per una creu formada per cinc quadrats.[6][7]
|
 |
1,4649 |
Corba quadràtica de Koch (tipus 1) |
 |
Es pot reconèixer en aquest fractal el fractal de Vicsek.[8]
|
 |
1,5000 |
Corba quadràtica de Koch (tipus 2) |
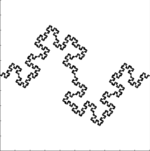 |
També coneguda com "salsitxa de Minkowski".[8]
|
![{\displaystyle \textstyle {\frac {\log \left({\frac {1+{\sqrt[{3}]{73-6{\sqrt {87}}}}+{\sqrt[{3}]{73+6{\sqrt {87}}}}}{3}}\right)}{\log(2)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76da064445f98d093fb3794b52656ab55745eeef) |
1.5236 |
Frontera de la corba del drac |
 |
Cf Chang & Zhang.[9][10]
|
 |
1.585 |
Arbre de tres branques |
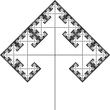   |
Cada branca es divideix en altres tres (en les representacions, amb angles de 90°, 60° i 120°). La dimensió fractal de l'arbre és la dimensió fractal de les ramas terminals.
|
 |
1.585 |
Triangle de Sierpinski |
 |
Pot ser generat per un sistema de Lindenmayer.[11]També, el triangle de Pascal mòdul 2.
|
 |
1.585 |
Corba de punta de fletxa de Sierpiński |
 |
Amb el mateix límit que el triangle de dalt però, construït a partir d'una corba unidimensional.
|
 |
1.6309 |
Triangle de Pascal mòdul 3 |
 |
Per a un triangle mòdul k, si k és primer, la dimensió fractal és  (Cf Stephen Wolfram).[12] (Cf Stephen Wolfram).[12]
|
 |
1.6379 |
Fractal de Fibonacci |
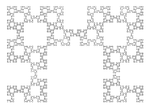 |
Fractal basat en la paraula de Fibonacci (o successió dels conills) Sloane A005614. Representació: Fractal després de 23 iteracions (F23=28657 segments).[13]
|
 |
1,6826 |
Triangle de Pascal mòdulo 5 |
 |
Per a un triangle mòdul k, si k és primer, la dimensió fractal és  (Cf Stephen Wolfram).[12] (Cf Stephen Wolfram).[12]
|
 |
1,7712 |
Hexafloc |
 |
En cada iteració es canvia cada hexàgon per un floc de 7 hexàgons. La seva frontera és el floc de neu de von Koch i conté infinits flocs de neu de Koch (blancs i negres).
|
 |
1.7712 |
Fractal H-I de Rivera |
 |
Fractal amb autosemblança exacta.
|
 |
1.7848 |
Corba de von Koch a 85°, fractal de Cesàro |
 |
Generalització de la corba de von Koch amb angle a entre 0 i 90°. La dimensió fractal és  .[8] .[8]
|
 |
1.8617 |
Pentafloc |
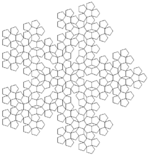 |
En cada iteració es canvia cada pentàgon per un floc de 6 pentàgons.  = raó àuria = = raó àuria =  . .
|
 |
1.8928 |
Catifa de Sierpinski |
 |
Cada una de les cares de l'esponja de Menger és una catifa de Sierpinski, com també ho és la superfície inferior de la superfície de Koch quadràtica tridimensional (tipus 1). Es pot construir per substitució de cadenes (string rewriting) i com l'atractor d'un sistema de funcions iterades.[14][15]
|
 |
1.8928 |
Pols de Cantor tridimensional |
 |
Conjunt de Cantor en tres dimensions.
|
| Estimat |
1.9340 |
Frontera de la corba de Lévy |
 |
Estimat per Duvall i Keesling (1999). La pròpia corba té una dimensió fractal de 2.
|
|
1,974 |
Tessel·lació de Penrose |
 |
Vegeu Ramachandrarao, Sinha & Sanyal.[16]
|
 |
2 |
Frontera del conjunt de Mandelbrot |
 |
La frontera i el propi conjunt tenen la mateixa dimensió.[17]
|
 |
2 |
Conjunt de Julia |
 |
Per a determinats valors de c (inclòs c pertanyent a la frontera del conjunt de Mandelbrot), el conjunt de Julia té una dimensió de 2.[18]
|
 |
2 |
Corba de Sierpiński |
 |
Tota corba de Peano que omple el pla té una dimensió de Hausdorff de 2.
|
 |
2 |
Corba de Hilbert |
 |
|
 |
2 |
Corba de Peano |
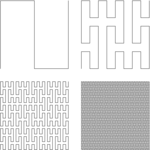 |
Així com tota una família de corbes construïdes de forma similar, com les corbes de Wunderlich.
|
 |
2 |
Corba de Moore |
 |
Es pot estendre a 3 dimensions.
|
|
2 |
Corba de Lebesgue o d'ordre z |
 |
A diferència de les anteriors, aquesta corba que omple el pla és diferenciable gairebé per tot. També, es pot definir altre tipus en dos dimensions. De la mateixa manera que la corba de Hilbert, es pot estendre a tres dimensions.[19]
|
 |
2 |
Corba del drac |
 |
La seva frontera té una dimensió fractal de 1.5236270862.[20]
|
|
2 |
Corba del terdrac |
 |
L-sistema: F→F+F–F, angle=120°.
|
 |
2 |
T-quadrat |
 |
|
 |
2 |
Corba de Gosper |
 |
La seva frontera és l'illa de Gosper.
|
 |
2 |
Tetraedre de Sierpinski |
 |
Cada tetraedre es substitueix per quatre tetraedres.
|
 |
2 |
Fractal H |
 |
També, l'«arbre de Mandelbrot», que mostra un patró semblant.
|
 |
2 |
Arbre de Pitàgores |
 |
Cada quadrat genera dos quadrats amb un factor de contracció de  .[21] .[21]
|
 |
2 |
Creu grega fractal en 2D |
 |
Cada segment es reemplaça per una creu formada per 4 segments.
|
|
2.06 |
Atractor de Lorenz |
 |
Per a determinats valors dels paràmetres.
|
 |
2.3296 |
Dodecaedro fractal |
 |
Cada dodecaedre es substitueix per 20 dodecaedres més petits.
|
 |
2.3347 |
Superfície quadràtica tridimensional de Koch (tipus 1) |
 |
Extensió tridimensional de la corba quadràtica de Koch (tipus 1). La representació mostra la segona iteració.
|
|
2.4739 |
Intersticis entre les esferes d'Apol·loni |
 |
Intersticis entre les esferes d'Apol·loni, equivalent tridimensional del cercle d'Apol·loni. Dimensió calculada per M. Borkovec, W. De Paris i R. Peikert.[22]
|
 |
2.50 |
Superfície quadràtica tridimensional de Koch (tipus 2) |
 |
Extensió tridimensional de la corba quàdrática de Koch (tipus 2). La representació mostra la segona iteració.
|
 |
2.5819 |
Icosàedre fractal |
 |
Cada icosàedre es substitueix per 12 icosàedres més petits.
|
 |
2.5849 |
Creu grega fractal en 3D |
 |
Cada segment es substitueix per una creu tridimensional formada per 6 segments.
|
 |
2.5849 |
Octàedre fractal |
 |
Cada octàedre es substitueix per 6 octàedres més petits.
|
 |
2.5849 |
Superfície de Koch |
 |
Cada triangle equilàter es substitueix per sis triangles equilàters de la meitat de mida.
|
 |
2,7268 |
Esponja de Menger |
 |
La seva superfície té una dimensió fractal de  . .
|
 |
3 |
Corba de Hilbert en 3D |
 |
Extensió de la corba de Hilbert a 3 dimensions.
|
 |
3 |
Corba de Lebesgue en 3D |
 |
Extensió de la corba de Lebesgue a 3 dimensions.
|
 |
3 |
Corba de Moore en 3D |
 |
Extensió de la corba de Moore a 3 dimensions.
|