| –Ę–į–∑–ł —Ā—ā–į—ā–ł—Ź —Ā–Ķ –Ĺ—É–∂–ī–į–Ķ –ĺ—ā –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä —Ā –Ņ–ĺ-–∑–į–ī—ä–Ľ–Ī–ĺ—á–Ķ–Ĺ–ł –Ņ–ĺ–∑–Ĺ–į–Ĺ–ł—Ź. –ź–ļ–ĺ —Ā–ľ—Ź—ā–į—ā–Ķ, —á–Ķ –ł–ľ–į—ā–Ķ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ł—ā–Ķ –∑–Ĺ–į–Ĺ–ł—Ź, –Ņ–ĺ–ī–ĺ–Ī—Ä–Ķ—ā–Ķ —ā–į–∑–ł —Ā—ā—Ä–į–Ĺ–ł—Ü–į. |
–ė–≥—Ä–į—ā–į ‚Äě–Ė–ł–≤–ĺ—ā‚Äú (–Ĺ–į –į–Ĺ–≥–Ľ–ł–Ļ—Ā–ļ–ł: Game of Life, Conway's Game of Life) –Ķ –Ņ–ĺ–Ņ—É–Ľ—Ź—Ä–Ĺ–į –ł–≥—Ä–į —Ā –Ĺ—É–Ľ–į –Ĺ–į –Ī—Ä–ĺ–Ļ –ł–≥—Ä–į—á–ł, –ł–∑–ľ–ł—Ā–Ľ–Ķ–Ĺ–į –Ņ—Ä–Ķ–∑ 1970 –≥–ĺ–ī–ł–Ĺ–į –ĺ—ā –Ē–∂–ĺ–Ĺ –•–ĺ—Ä—ā—ä–Ĺ –ö–ĺ–Ĺ—É–Ķ–Ļ (–Ĺ–į –į–Ĺ–≥–Ľ–ł–Ļ—Ā–ļ–ł: John Horton Conway), –ļ–ĺ—Ź—ā–ĺ –Ķ –Ĺ–į–Ļ-–ł–∑–≤–Ķ—Ā—ā–Ĺ–ł—Ź—ā –Ņ—Ä–ł–ľ–Ķ—Ä –∑–į –ļ–Ľ–Ķ—ā—ä—á–Ķ–Ĺ –į–≤—ā–ĺ–ľ–į—ā. –ü—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ł–≥—Ä–į—ā–į –Ķ (–ļ—Ä–į–Ļ–Ĺ–į –ł–Ľ–ł –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–į) –ī–≤—É–ľ–Ķ—Ä–Ĺ–į —Ä–Ķ—ą–Ķ—ā–ļ–į –ĺ—ā –ļ–≤–į–ī—Ä–į—ā–Ĺ–ł –ļ–Ľ–Ķ—ā–ļ–ł, –≤—Ā—Ź–ļ–į –ĺ—ā –ļ–ĺ–ł—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ĺ–į–ľ–ł—Ä–į –≤ –Ķ–ī–Ĺ–ĺ –ĺ—ā –ĺ–Ī—Č–ĺ –ī–≤–Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ł —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł—Ź: –∂–ł–≤–į –ł–Ľ–ł –ľ—ä—Ä—ā–≤–į. –í—Ā—Ź–ļ–į –ļ–Ľ–Ķ—ā–ļ–į –ĺ—ā —Ä–Ķ—ą–Ķ—ā–ļ–į—ā–į –≤–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–į —Ā –ĺ—Ā–Ķ–ľ—ā–Ķ —Ā–ł —Ā—ä—Ā–Ķ–ī–į: —Ā—ä—Ā–Ķ–ī–Ĺ–ł—ā–Ķ –ļ–Ľ–Ķ—ā–ļ–ł –Ņ–ĺ —Ö–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ, –≤–Ķ—Ä—ā–ł–ļ–į–Ľ –ł –ī–ł–į–≥–ĺ–Ĺ–į–Ľ. –Ě–į –ł—ā–Ķ—Ä–į—ā–ł–≤–Ķ–Ĺ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ, —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –≤—Ā—Ź–ļ–į –ļ–Ľ–Ķ—ā–ļ–į –≤ —Ä–Ķ—ą–Ķ—ā–ļ–į—ā–į –∑–į–Ņ–į–∑–≤–į –ł–Ľ–ł –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ —Ā–ł –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā –ĺ—ā –Ņ—Ä–Ķ–ī–≤–į—Ä–ł—ā–Ķ–Ľ–Ĺ–ĺ –∑–į–ī–į–ī–Ķ–Ĺ —Ā–Ņ–ł—Ā—ä–ļ –ĺ—ā –Ņ—Ä–į–≤–ł–Ľ–į.
–ė–≥—Ä–į—ā–į –Ķ –Ņ—Ä–ł–ľ–Ķ—Ä –∑–į —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā–ł –ļ–į—ā–ĺ –≤—ä–∑–Ĺ–ł–ļ–≤–į–Ĺ–Ķ (—Ā–į–ľ–ĺ–Ņ–ĺ—Ä–į–∂–ī–į–Ĺ–Ķ) –ł —Ā–į–ľ–ĺ–ĺ—Ä–≥–į–Ĺ–ł–∑–į—Ü–ł—Ź. –° –ī–Ķ–ľ–ĺ–Ĺ—Ā—ā—Ä–į—Ü–ł—Ź—ā–į –Ĺ–į —ā–ĺ–≤–į –ļ–į–ļ –ĺ—ā –Ņ—Ä–ł–Ľ–į–≥–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –Ņ—Ä–ĺ—Ā—ā–ł –Ņ—Ä–į–≤–ł–Ľ–į —Ā–Ķ –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į—ā —Ā–Ľ–ĺ–∂–Ĺ–ł —Ā—ā—Ä—É–ļ—ā—É—Ä–ł —ā—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā –∑–į —Ą–ł–∑–ł—Ü–ł, –Ī–ł–ĺ–Ľ–ĺ–∑–ł, –ł–ļ–ĺ–Ĺ–ĺ–ľ–ł—Ā—ā–ł, –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł, —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą–ł –ł —É—á–Ķ–Ĺ–ł –ĺ—ā –ī—Ä—É–≥–ł –Ĺ–į—É—á–Ĺ–ł –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź.
–ü—Ä–ĺ–ł–∑—Ö–ĺ–ī
–ö–ĺ–Ĺ—É–Ķ–Ļ –Ķ –Ī–ł–Ľ –∑–į–ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–ĺ–≤–į–Ĺ –ĺ—ā –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ, –Ņ–ĺ—Ā—ā–į–≤–Ķ–Ĺ –Ņ—Ä–Ķ–∑ 1940-—ā–Ķ –ĺ—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į –Ē–∂–ĺ–Ĺ —Ą–ĺ–Ĺ –Ě–ĺ–Ļ–ľ–į–Ĺ, –ļ–ĺ–Ļ—ā–ĺ —Ā–Ķ –Ķ –ĺ–Ņ–ł—ā–į–Ľ –ī–į —Ä–į–∑—Ä–į–Ī–ĺ—ā–ł —Ö–ł–Ņ–ĺ—ā–Ķ—ā–ł—á–Ĺ–į –ľ–į—ą–ł–Ĺ–į, –ļ–ĺ—Ź—ā–ĺ –ī–į –ľ–ĺ–∂–Ķ –ī–į —Ā—ä–∑–ī–į–≤–į –ļ–ĺ–Ņ–ł—Ź –Ĺ–į —Ā–Ķ–Ī–Ķ —Ā–ł. –£—Ā–Ņ—Ź–≤–į, –ļ–ĺ–≥–į—ā–ĺ –Ĺ–į–ľ–ł—Ä–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ľ–ĺ–ī–Ķ–Ľ –∑–į —ā–į–ļ–į–≤–į –ľ–į—ą–ł–Ĺ–į —Ā –ł–∑–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ĺ–ĺ —Ā–Ľ–ĺ–∂–Ĺ–ł –Ņ—Ä–į–≤–ł–Ľ–į –ł –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–į —Ä–Ķ—ą–Ķ—ā–ļ–į. ‚Äě–Ė–ł–≤–ĺ—ā‚Äú –Ķ —Ä–Ķ–∑—É–Ľ—ā–į—ā –ĺ—ā —É—Ā–Ņ–Ķ—ą–Ĺ–ł—Ź –ĺ–Ņ–ł—ā –Ĺ–į –ö–ĺ–Ĺ—É–Ķ–Ļ –ī–į –ĺ–Ņ—Ä–ĺ—Ā—ā–ł –ī—Ä–į—Ā—ā–ł—á–Ĺ–ĺ –ł–ī–Ķ–ł—ā–Ķ –Ĺ–į —Ą–ĺ–Ĺ –Ě–ĺ–Ļ–ľ–į–Ĺ. –ė–≥—Ä–į—ā–į –ł–∑–Ľ–ł–∑–į –∑–į –Ņ—Ä—ä–≤ –Ņ—ä—ā –≤ Scientific American –Ņ—Ä–Ķ–∑ –ĺ–ļ—ā–ĺ–ľ–≤—Ä–ł 1970 –≤ –ļ–ĺ–Ľ–ĺ–Ĺ–ļ–į—ā–į –Ĺ–į –ú–į—Ä—ā–ł–Ĺ –ď–į—Ä–ī–Ĺ—ä—Ä ‚Äě–ú–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ł–≥—Ä–ł‚Äú. –ě—ā —ā–Ķ–ĺ—Ä–Ķ—ā–ł—á–Ĺ–į –≥–Ľ–Ķ–ī–Ĺ–į —ā–ĺ—á–ļ–į –ł–≥—Ä–į—ā–į –Ķ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ–į, –∑–į—Č–ĺ—ā–ĺ –ł–ľ–į —Ā–≤–ĺ–Ļ—Ā—ā–≤–į—ā–į –Ĺ–į —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ–Ĺ–į—ā–į –ľ–į—ą–ł–Ĺ–į –Ĺ–į –Ę—é—Ä–ł–Ĺ–≥, –ļ–ĺ–Ķ—ā–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ –≤—Ā–ł—á–ļ–ĺ, –ļ–ĺ–Ķ—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ņ—Ä–ĺ–≥—Ä–į–ľ–ł—Ä–į–Ĺ–ĺ –Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–ĺ–ľ –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ, –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ņ—Ä–ĺ–≥—Ä–į–ľ–ł—Ä–į–Ĺ–ĺ —Ā ‚Äě–Ė–ł–≤–ĺ—ā‚Äú. –ď–į—Ä–ī–Ĺ—ä—Ä –Ņ–ł—ą–Ķ:
| ‚Äě
|
–ė–≥—Ä–į—ā–į –Ņ—Ä–į–≤–ł –ö–ĺ–Ĺ—É–Ķ–Ļ –ł–∑–≤–Ķ—Ā—ā–Ķ–Ĺ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į–Ľ–Ĺ–ĺ, –Ĺ–ĺ —Ā—ä—Č–ĺ —ā–į–ļ–į –ĺ—ā–≤–į—Ä—Ź —Ü—Ź–Ľ–į –Ĺ–ĺ–≤–į –ĺ–Ī–Ľ–į—Ā—ā –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ—ā–ĺ –Ņ—Ä–ĺ—É—á–≤–į–Ĺ–Ķ ‚Äď –ĺ–Ī–Ľ–į—Ā—ā—ā–į –Ĺ–į –ļ–Ľ–Ķ—ā—ä—á–Ĺ–ł—ā–Ķ –į–≤—ā–ĺ–ľ–į—ā–ł. –ü–ĺ—Ä–į–ī–ł –į–Ĺ–į–Ľ–ĺ–≥–ł—Ź—ā–į –Ĺ–į ‚Äě–Ė–ł–≤–ĺ—ā‚Äú —Ā –Ņ–ĺ—Ź–≤–į—ā–į, –Ņ–į–ī–į –ł –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ł—ā–Ķ –Ĺ–į –Ķ–ī–Ĺ–ĺ –ĺ–Ī—Č–Ķ—Ā—ā–≤–ĺ –ĺ—ā –∂–ł–≤–ł –ĺ—Ä–≥–į–Ĺ–ł–∑–ľ–ł, –ł–≥—Ä–į—ā–į –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–ł –ļ—ä–ľ —Ä–į–∑–≤–ł–≤–į—Č–ł—Ź —Ā–Ķ –∂–į–Ĺ—Ä –Ĺ–į —ā–į–ļ–į –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–ł—ā–Ķ ‚Äě–ł–≥—Ä–ł —Ā–ł–ľ—É–Ľ–į—Ü–ł–ł‚Äú (–ł–≥—Ä–ł, –ļ–ĺ–ł—ā–ĺ –Ņ—Ä–Ķ—Ā—ä–∑–ī–į–≤–į—ā –Ņ—Ä–ĺ—Ü–Ķ—Ā–ł –ĺ—ā –ł—Ā—ā–ł–Ĺ—Ā–ļ–ł—Ź –∂–ł–≤–ĺ—ā).
|
“
|
–ě—ā –Ņ—É–Ī–Ľ–ł–ļ–į—Ü–ł—Ź—ā–į —Ā–ł –Ĺ–į—Ā–į–ľ, ‚Äě–Ė–ł–≤–ĺ—ā‚Äú –Ņ—Ä–ł–≤–Ľ–ł—á–į –≥–ĺ–Ľ—Ź–ľ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā —Ā –ł–∑–Ĺ–Ķ–Ĺ–į–ī–≤–į—Č–ł—ā–Ķ –Ĺ–į—á–ł–Ĺ–ł, –Ņ–ĺ –ļ–ĺ–ł—ā–ĺ –ľ–ĺ–≥–į—ā –ī–į –Ķ–≤–ĺ–Ľ—é–ł—Ä–į—ā —Ā—ä–∑–ī–į–ī–Ķ–Ĺ–ł—ā–Ķ –ľ–ĺ–ī–Ķ–Ľ–ł. ‚Äě–Ė–ł–≤–ĺ—ā‚Äú –Ņ—Ä–Ķ–ī–ĺ—Ā—ā–į–≤—Ź –Ņ—Ä–ł–ľ–Ķ—Ä –∑–į –Ņ–ĺ—Ä–į–∂–ī–į–Ĺ–Ķ –ł —Ā–į–ľ–ĺ–ĺ—Ä–≥–į–Ĺ–ł–∑–į—Ü–ł—Ź. –£—á–Ķ–Ĺ–ł –≤ —Ä–į–∑–Ľ–ł—á–Ĺ–ł —Ā—Ą–Ķ—Ä–ł (–ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–ł –Ĺ–į—É–ļ–ł, —Ą–ł–∑–ł–ļ–į, –Ī–ł–ĺ–Ľ–ĺ–≥–ł—Ź, –Ī–ł–ĺ—Ö–ł–ľ–ł—Ź, –ł–ļ–ĺ–Ĺ–ĺ–ľ–ł–ļ–į, –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į, —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą–ł—Ź –ł –≥–Ķ–Ĺ–Ķ—Ä–į—ā–ł–≤–Ĺ–ł –Ĺ–į—É–ļ–ł) –ł–∑–≤–Ľ–ł—á–į—ā –Ņ–ĺ–Ľ–∑–į –ĺ—ā –Ĺ–į—á–ł–Ĺ–į, –Ņ–ĺ –ļ–ĺ–Ļ—ā–ĺ –ĺ—ā –Ņ—Ä–ł–Ľ–į–≥–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –Ņ—Ä–ĺ—Ā—ā–ł—ā–Ķ –Ņ—Ä–į–≤–ł–Ľ–į –Ĺ–į –ł–≥—Ä–į—ā–į –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź—ā —Ā–Ľ–ĺ–∂–Ĺ–ł –ľ–ĺ–ī–Ķ–Ľ–ł. –ė–≥—Ä–į—ā–į —Ā—ä—Č–ĺ —ā–į–ļ–į –ľ–ĺ–∂–Ķ –ī–į —Ā–Ľ—É–∂–ł –ļ–į—ā–ĺ –Ņ–ĺ—É—á–ł—ā–Ķ–Ľ–Ĺ–į –į–Ĺ–į–Ľ–ĺ–≥–ł—Ź, –ļ–ĺ—Ź—ā–ĺ –ī–į –Ņ–ĺ–ļ–į–∑–≤–į –ī–ĺ–Ĺ—Ź–ļ—ä–ī–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–į—ā–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–į, —á–Ķ ‚Äě–ī–ł–∑–į–Ļ–Ĺ‚Äú –ł ‚Äě–ĺ—Ä–≥–į–Ĺ–ł–∑–į—Ü–ł—Ź‚Äú –ľ–ĺ–≥–į—ā –ī–į –≤—ä–∑–Ĺ–ł–ļ–Ĺ–į—ā —Ā–Ņ–ĺ–Ĺ—ā–į–Ĺ–Ĺ–ĺ –≤ –ĺ—ā—Ā—ä—Ā—ā–≤–ł–Ķ—ā–ĺ –Ĺ–į –ī–ł–∑–į–Ļ–Ĺ–Ķ—Ä/—Ā—ä–∑–ī–į—ā–Ķ–Ľ. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä –Ē–į–Ĺ–ł–Ķ–Ľ –Ē–Ķ–Ĺ–Ķ—ā, —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą –ł –ļ–ĺ–≥–Ĺ–ł—ā–ł–≤–Ķ–Ĺ —É—á–Ķ–Ĺ, –ł–∑–Ņ–ĺ–Ľ–∑–≤–į –į–Ĺ–į–Ľ–ĺ–≥–ł—Ź—ā–į —Ā –≤—Ā–Ķ–Ľ–Ķ–Ĺ–į—ā–į –Ĺ–į ‚Äě–Ė–ł–≤–ĺ—ā‚Äú, –∑–į –ī–į –Ņ–ĺ–ļ–į–∂–Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–į—ā–į –Ķ–≤–ĺ–Ľ—é—Ü–ł—Ź –Ĺ–į —Ā–Ľ–ĺ–∂–Ĺ–ł —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą—Ā–ļ–ł –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł–ł –ļ–į—ā–ĺ —Ā—ä–∑–Ĺ–į–Ĺ–ł–Ķ –ł —Ā–≤–ĺ–Ī–ĺ–ī–Ĺ–į –≤–ĺ–Ľ—Ź –ĺ—ā –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā–ł—Ź –Ĺ–į–Ī–ĺ—Ä –ī–Ķ—ā–Ķ—Ä–ľ–ł–Ĺ–ł—Ā—ā–ł—á–Ĺ–ł —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł –∑–į–ļ–ĺ–Ĺ–ł, –ļ–ĺ–ł—ā–ĺ –ī–Ķ–Ļ—Ā—ā–≤–į—ā –≤ –Ĺ–į—ą–į—ā–į –≤—Ā–Ķ–Ľ–Ķ–Ĺ–į.
–ü–ĺ–Ņ—É–Ľ—Ź—Ä–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į ‚Äě–Ė–ł–≤–ĺ—ā‚Äú –Ķ –Ņ–ĺ–ī–Ņ–ĺ–ľ–ĺ–≥–Ĺ–į—ā–į –ĺ—ā –Ņ–ĺ—Ź–≤–į—ā–į —Ě —ā–ĺ—á–Ĺ–ĺ –≤ –ľ–ĺ–ľ–Ķ–Ĺ—ā, –≤ –ļ–ĺ–Ļ—ā–ĺ –Ĺ–į –Ņ–į–∑–į—Ä–į —Ā–į –Ņ—É—Ā–Ĺ–į—ā–ł –Ĺ–ĺ–≤–ĺ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł–Ķ –ī–ĺ—Ā—ā—ä–Ņ–Ĺ–ł –ľ–ł–Ĺ–ł–ļ–ĺ–ľ–Ņ—é—ā—Ä–ł. –ė–≥—Ä–į—ā–į –Ķ –ľ–ĺ–∂–Ķ–Ľ–į –ī–į –≤—ä—Ä–≤–ł —Ā —á–į—Ā–ĺ–≤–Ķ –Ĺ–į —ā–Ķ–∑–ł –ľ–į—ą–ł–Ĺ–ł, –ļ–ĺ–ł—ā–ĺ –ł–Ĺ–į—á–Ķ –Ī–ł—Ö–į –ĺ—Ā—ā–į–Ĺ–į–Ľ–ł –Ĺ–Ķ–ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ĺ–ł –Ĺ–ĺ—Č–Ķ–ľ. –í —ā–ĺ–≤–į –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –ł–≥—Ä–į—ā–į –Ņ—Ä–Ķ–ī–≤–Ķ—Č–į–≤–į –Ņ–ĺ-–ļ—ä—Ā–Ĺ–į—ā–į –Ņ–ĺ–Ņ—É–Ľ—Ź—Ä–Ĺ–ĺ—Ā—ā –Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–ĺ –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į–Ĺ–ł —Ą—Ä–į–ļ—ā–į–Ľ–ł. –ó–į –ľ–Ĺ–ĺ–≥–ĺ ‚Äě–Ė–ł–≤–ĺ—ā‚Äú –Ķ –Ņ—Ä–ĺ—Ā—ā–ĺ —Ā–ĺ—Ą—ā—É–Ķ—Ä–Ĺ–ĺ –Ņ—Ä–Ķ–ī–ł–∑–≤–ł–ļ–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ ‚Äď –∑–į–Ī–į–≤–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ –ī–į —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į –ł–Ĺ–į—á–Ķ –Ņ—Ä–į—Ö–ĺ—Ā–į–Ĺ–ĺ –≤—Ä–Ķ–ľ–Ķ –Ĺ–į –Ņ—Ä–ĺ—Ü–Ķ—Ā–ĺ—Ä–į. –ó–į –ī—Ä—É–≥–ł –ĺ–Ī–į—á–Ķ, ‚Äě–Ė–ł–≤–ĺ—ā‚Äú –ł–ľ–į –Ņ–ĺ-—Ą–ł–Ľ–ĺ—Ā–ĺ—Ą—Ā–ļ–ĺ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ. –ě–ļ–ĺ–Ľ–ĺ –Ĺ–Ķ—Ź –Ņ—Ä–Ķ–∑ 1970-—ā–Ķ –ł –Ņ–ĺ-–ļ—ä—Ā–Ĺ–ĺ –Ķ —Ā—Ą–ĺ—Ä–ľ–ł—Ä–į–Ĺ –ļ—É–Ľ—ā. –Ę–Ķ–ļ—É—Č–ł—ā–Ķ —Ä–į–∑—Ä–į–Ī–ĺ—ā–ļ–ł —Ā–į —Ā—ā–ł–≥–Ĺ–į–Ľ–ł —ā–ĺ–Ľ–ļ–ĺ–≤–į –ī–į–Ľ–Ķ—á, —á–Ķ —Ā–Ķ —Ā—ä–∑–ī–į–≤–į—ā —ā–Ķ–ĺ—Ä–Ķ—ā–ł—á–Ĺ–ł –Ķ–ľ—É–Ľ–į—Ü–ł–ł –Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ–ł, –≤–ľ–Ķ—Ā—ā–Ķ–Ĺ–ł –≤ —Ä–į–ľ–ļ–ł—ā–Ķ –Ĺ–į ‚Äě–Ė–ł–≤–ĺ—ā‚Äú.
–ö–ĺ–Ĺ—É–Ķ–Ļ –ł–∑–Ī–ł—Ä–į –Ņ—Ä–į–≤–ł–Ľ–į—ā–į –≤–Ĺ–ł–ľ–į—ā–Ķ–Ľ–Ĺ–ĺ, —Ā–Ľ–Ķ–ī –∑–Ĺ–į—á–ł—ā–Ķ–Ľ–Ĺ–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –Ķ–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā–ł, —ā–į–ļ–į —á–Ķ –ī–į –ĺ—ā–≥–ĺ–≤–į—Ä—Ź—ā –Ĺ–į —Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ –ļ—Ä–ł—ā–Ķ—Ä–ł–ł:
- –Ě–Ķ —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į —Ä—Ź–∑—ä–ļ —Ä–į—Ā—ā–Ķ–∂.
- –Ę—Ä—Ź–Ī–≤–į –ī–į —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –ľ–į–Ľ–ļ–ł –Ĺ–į—á–į–Ľ–Ĺ–ł –ľ–ĺ–ī–Ķ–Ľ–ł —Ā —Ö–į–ĺ—ā–ł—á–Ĺ–ĺ, –Ĺ–Ķ–Ņ—Ä–Ķ–ī—Ā–ļ–į–∑—É–Ķ–ľ–ĺ —Ä–į–∑–≤–ł—ā–ł–Ķ.
- –Ę—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į –Ņ–ĺ—ā–Ķ–Ĺ—Ü–ł–į–Ľ –∑–į —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ–Ĺ–ł –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–ĺ—Ä–ł –Ĺ–į —Ą–ĺ–Ĺ –Ě–ĺ–Ļ–ľ–į–Ĺ (–≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā –∑–į —Ā–į–ľ–ĺ—Ä–į–∑–≤–ł—ā–ł–Ķ).
- –ü—Ä–į–≤–ł–Ľ–į—ā–į —ā—Ä—Ź–Ī–≤–į –ī–į —Ā–į –ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ –Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ-–Ņ—Ä–ĺ—Ā—ā–ł –ł –ī–į —Ā–Ķ –Ņ—Ä–ł–ī—ä—Ä–∂–į—ā –ļ—ä–ľ –≥–ĺ—Ä–Ķ–Ņ–ĺ—Ā–ĺ—á–Ķ–Ĺ–ł—ā–Ķ –Ņ—Ä–į–≤–ł–Ľ–į.
–ü—Ä–į–≤–ł–Ľ–į
–ě—Ä–ł–≥–ł–Ĺ–į–Ľ–Ĺ–ł—ā–Ķ –Ņ—Ä–į–≤–ł–Ľ–į –Ĺ–į –ł–≥—Ä–į—ā–į ‚Äě–Ė–ł–≤–ĺ—ā‚Äú —Ā–į —Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ:
- –í—Ā—Ź–ļ–į –∂–ł–≤–į –ļ–Ľ–Ķ—ā–ļ–į —Ā –Ņ–ĺ-–ľ–į–Ľ–ļ–ĺ –ĺ—ā –ī–≤–Ķ –∂–ł–≤–ł —Ā—ä—Ā–Ķ–ī–Ĺ–ł –ļ–Ľ–Ķ—ā–ļ–ł —É–ľ–ł—Ä–į (–ĺ—ā —Ā–į–ľ–ĺ—ā–į).
- –í—Ā—Ź–ļ–į –∂–ł–≤–į –ļ–Ľ–Ķ—ā–ļ–į —Ā –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā —ā—Ä–ł –∂–ł–≤–ł —Ā—ä—Ā–Ķ–ī–Ĺ–ł –ļ–Ľ–Ķ—ā–ļ–ł —É–ľ–ł—Ä–į (–ĺ—ā –Ņ—Ä–Ķ–Ĺ–į—Ā–Ķ–Ľ–Ķ–Ĺ–ĺ—Ā—ā).
- –í—Ā—Ź–ļ–į –∂–ł–≤–į –ļ–Ľ–Ķ—ā–ļ–į —Ā –ī–≤–Ķ –ł–Ľ–ł —ā—Ä–ł –∂–ł–≤–ł —Ā—ä—Ā–Ķ–ī–Ĺ–ł –ļ–Ľ–Ķ—ā–ļ–ł –ĺ—Ā—ā–į–≤–į –∂–ł–≤–į –ł –Ĺ–į —Ā–Ľ–Ķ–ī–≤–į—Č–į—ā–į –ł—ā–Ķ—Ä–į—Ü–ł—Ź.
- –í—Ā—Ź–ļ–į –ľ—ä—Ä—ā–≤–į –ļ–Ľ–Ķ—ā–ļ–į —Ā —ā–ĺ—á–Ĺ–ĺ —ā—Ä–ł –∂–ł–≤–ł —Ā—ä—Ā–Ķ–ī–Ĺ–ł –ļ–Ľ–Ķ—ā–ļ–ł —Ā–Ķ –Ņ—Ä–Ķ–≤—Ä—ä—Č–į –≤ –∂–ł–≤–į –ļ–Ľ–Ķ—ā–ļ–į.
–Ę–Ķ–∑–ł –Ņ—Ä–į–≤–ł–Ľ–į –ľ–ĺ–≥–į—ā –ī–į —ā—ä—Ä–Ņ—Ź—ā –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –ľ–ĺ–ī–ł—Ą–ł–ļ–į—Ü–ł–ł –Ņ–ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā–ł—ā–Ķ, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—Č–ł —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –ī–į–ī–Ķ–Ĺ–į –ļ–Ľ–Ķ—ā–ļ–į.
–Ě–į—á–į–Ľ–Ĺ–ĺ—ā–ĺ —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –Ĺ–į –Ņ–ĺ–Ľ–Ķ—ā–ĺ —Ā–Ķ —Ä–į–∑–≥–Ľ–Ķ–∂–ī–į –ļ–į—ā–ĺ —Ā–≤–ĺ–Ķ–ĺ–Ī—Ä–į–∑–Ķ–Ĺ –Ņ–ĺ—Ā–Ķ–≤. –Ě–į –≤—Ā—Ź–ļ–į –ł—ā–Ķ—Ä–į—Ü–ł—Ź (–ĺ—Č–Ķ –Ĺ–į—Ä–ł—á–į–Ĺ–į ‚Äě–≥–Ķ–Ĺ–Ķ—Ä–į—Ü–ł—Ź‚Äú, ‚Äě–Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł–Ķ‚Äú) –Ņ—Ä–į–≤–ł–Ľ–į—ā–į –Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į—ā–į —Ā–Ķ –Ņ—Ä–ł–Ľ–į–≥–į—ā –Ķ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ –ļ—ä–ľ –≤—Ā—Ź–ļ–į –ĺ—ā–ī–Ķ–Ľ–Ĺ–į –ļ–Ľ–Ķ—ā–ļ–į –≤ –Ņ–ĺ–Ľ–Ķ—ā–ĺ –ł –Ĺ–ĺ–≤–ł—ā–Ķ ‚Äě—Ä–į–∂–ī–į–Ĺ–ł—Ź‚Äú –ł ‚Äě—Ā–ľ—ä—Ä—ā–ł‚Äú –Ĺ–į –ļ–Ľ–Ķ—ā–ļ–ł—ā–Ķ —Ā–Ķ —Ā–Ľ—É—á–≤–į—ā –Ķ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ. –ü–ĺ —ā–ĺ–∑–ł –Ĺ–į—á–ł–Ĺ –≤—Ā—Ź–ļ–į –ł—ā–Ķ—Ä–į—Ü–ł—Ź –Ķ —Ą—É–Ĺ–ļ—Ü–ł—Ź, –∑–į–≤–ł—Ā–Ķ—Č–į —Ā–į–ľ–ĺ –ĺ—ā —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į—ā–į –ĺ—ā –Ņ—Ä–Ķ–ī—Ö–ĺ–ī–Ĺ–į—ā–į –ł—ā–Ķ—Ä–į—Ü–ł—Ź, –ł –Ĺ—Ź–ľ–į –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā –Ĺ–į —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ—Ā—ā. –í —ā–ĺ–∑–ł —Ā–ľ–ł—Ā—ä–Ľ –ł–≥—Ä–į—ā–į –Ķ –∑–į –Ĺ—É–Ľ–į –ł–≥—Ä–į—á–ł: —ā–ĺ–≤–į –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ —Ä–į–∑–≤–ĺ—Ź—ā —Ě —Ā–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź —Ā–į–ľ–ĺ –ĺ—ā –Ĺ–į—á–į–Ľ–Ĺ–ĺ—ā–ĺ —Ě —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ, –Ī–Ķ–∑ –ī–į –Ķ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–į –Ĺ–į–ľ–Ķ—Ā–į –ĺ—ā —á–ĺ–≤–Ķ–ļ. –í–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–ł–Ķ—ā–ĺ –Ĺ–į —á–ĺ–≤–Ķ–ļ–į —Ā –ł–≥—Ä–į—ā–į —Ā–Ķ –ł–∑—á–Ķ—Ä–Ņ–≤–į —Ā—ä—Ā –∑–į–ī–į–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –Ĺ–į—á–į–Ľ–Ĺ–ł—ā–Ķ —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā–ł –Ĺ–į –ļ–Ľ–Ķ—ā–ļ–ł—ā–Ķ –≤ –Ņ–ĺ–Ľ–Ķ—ā–ĺ, –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —Ä–į–∑–≤–ł—ā–ł–Ķ—ā–ĺ —Ě –ł –Ķ–≤–Ķ–Ĺ—ā—É–į–Ľ–Ĺ–ĺ—ā–ĺ —Ě –Ņ—Ä–Ķ–ļ—ä—Ā–≤–į–Ĺ–Ķ —Ā–Ľ–Ķ–ī –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ –Ī—Ä–ĺ–Ļ –ł—ā–Ķ—Ä–į—Ü–ł–ł.
–ü—Ä–ł–ľ–Ķ—Ä–Ĺ–ł –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ł
–Ě–į–Ļ-—Ä–į–Ĺ–Ĺ–ł—ā–Ķ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ–ł –ľ–ĺ–ī–Ķ–Ľ–ł –≤ ‚Äě–Ė–ł–≤–ĺ—ā‚Äú —Ā–į –ĺ—ā–ļ—Ä–ł—ā–ł –Ī–Ķ–∑ —É–Ņ–ĺ—ā—Ä–Ķ–Ī–į—ā–į –Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä. –Ě–į–Ļ-–Ņ—Ä–ĺ—Ā—ā–ł—ā–Ķ —Ā—ā–į—ā–ł—á–Ĺ–ł –ľ–ĺ–ī–Ķ–Ľ–ł (still lifes) –ł –Ņ–ĺ–≤—ā–į—Ä—Ź–Ķ–ľ–ł –ľ–ĺ–ī–Ķ–Ľ–ł (–ĺ—Ā—Ü–ł–Ľ–į—ā–ĺ—Ä–ł) —Ā–į –ĺ—ā–ļ—Ä–ł—ā–ł –Ņ—Ä–ł –Ņ—Ä–ĺ—Ā–Ľ–Ķ–ī—Ź–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ä–į–∑–≤–ł—ā–ł–Ķ—ā–ĺ –Ĺ–į —Ä–į–∑–Ľ–ł—á–Ĺ–ł –ľ–į–Ľ–ļ–ł —Ā—ā–į—Ä—ā–ĺ–≤–ł –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ł, –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ļ–ļ–ł –ľ–ł–Ľ–ł–ľ–Ķ—ā—Ä–ĺ–≤–į —Ö–į—Ä—ā–ł—Ź, —á–Ķ—Ä–Ĺ–ł –ī—ä—Ā–ļ–ł, –ł–≥—Ä–ĺ–≤–ł –ī—ä—Ā–ļ–ł (–ļ–į—ā–ĺ –ł–≥—Ä–į—ā–į –ď–ĺ) –ł –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł. –ü–ĺ –≤—Ä–Ķ–ľ–Ķ –Ĺ–į —ā–ĺ–≤–į —Ä–į–Ĺ–Ĺ–ĺ –Ņ—Ä–ĺ—É—á–≤–į–Ĺ–Ķ, –ö–ĺ–Ĺ—É–Ķ–Ļ –ĺ—ā–ļ—Ä–ł–≤–į, —á–Ķ R-–Ņ–Ķ–Ĺ—ā–ĺ–ľ–ł–Ĺ–ĺ –Ĺ–Ķ —É—Ā–Ņ—Ź–≤–į –ī–į —Ā–Ķ —Ā—ā–į–Ī–ł–Ľ–ł–∑–ł—Ä–į –≤ –ľ–į–Ľ—ä–ļ –Ī—Ä–ĺ–Ļ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł—Ź. –í—Ā—ä—Č–Ĺ–ĺ—Ā—ā –ĺ—ā–Ĺ–Ķ–ľ–į 1103 –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł—Ź –ī–į —Ā–Ķ —Ā—ā–į–Ī–ł–Ľ–ł–∑–ł—Ä–į, –į –ī–ĺ—ā–ĺ–≥–į–≤–į –ł–ľ–į –Ņ–ĺ–Ņ—É–Ľ–į—Ü–ł—Ź –ĺ—ā 116 –ł –Ķ –ł–∑—Ā—ā—Ä–Ķ–Ľ—Ź–Ľ–į —ą–Ķ—Ā—ā ‚Äě–≥–Ľ–į–Ļ–ī–Ķ—Ä–į‚Äú (—ā–ĺ–≤–į —Ā–į —Ā—ā—Ä—É–ļ—ā—É—Ä–ł, –ļ–ĺ–ł—ā–ĺ –∑–į–Ņ–į–∑–≤–į—ā –Ņ–ĺ—É–Ľ–į—Ü–ł—Ź—ā–į —Ā–ł, –ļ–į—ā–ĺ —Ā–Ķ –Ņ—Ä–ł–ī–≤–ł–∂–≤–į—ā –≤ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–į –Ņ–ĺ—Ā–ĺ–ļ–į).
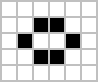
–ú–Ĺ–ĺ–≥–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ–ł —ā–ł–Ņ–ĺ–≤–Ķ –ľ–ĺ–ī–Ķ–Ľ–ł —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź–≤–į—ā –≤ ‚Äě–Ė–ł–≤–ĺ—ā‚Äú –≤–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ĺ–ĺ —Ā—ā–į—ā–ł—Ü–ł, –ĺ—Ā—Ü–ł–Ľ–į—ā–ĺ—Ä–ł –ł –ľ–ĺ–∑–į–Ļ–ļ–ł, –ļ–ĺ–ł—ā–ĺ —Ā–Ķ –Ņ—Ä–Ķ–Ĺ–į—Ā—Ź—ā –Ņ–ĺ –Ņ–ĺ–Ľ–Ķ—ā–ĺ, –ĺ–Ņ—Ä–ł–Ľ–ł—á–į–≤–į–Ĺ–ł –Ĺ–į –ļ–ĺ—Ā–ľ–ł—á–Ķ—Ā–ļ–ł –ļ–ĺ—Ä–į–Ī–ł –ł —Ā–ĺ–≤–į–Ľ–ļ–ł. –Ě—Ź–ļ–ĺ–ł —á–Ķ—Ā—ā–ĺ —Ā—Ä–Ķ—Č–į–Ĺ–ł –Ņ—Ä–ł–ľ–Ķ—Ä–ł –ĺ—ā —ā–Ķ–∑–ł —ā—Ä–ł –ļ–Ľ–į—Ā–į —Ā–į –Ņ–ĺ–ļ–į–∑–į–Ĺ–ł –Ņ–ĺ-–ī–ĺ–Ľ—É, –ļ—ä–ī–Ķ—ā–ĺ –∂–ł–≤–ł—ā–Ķ –ļ–Ľ–Ķ—ā–ļ–ł —Ā–į –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł –≤ —á–Ķ—Ä–Ĺ–ĺ, –į –ľ—ä—Ä—ā–≤–ł—ā–Ķ –≤ –Ī—Ź–Ľ–ĺ.
–°—ā–į—ā–ł—á–Ĺ–ł –ľ–ĺ–∑–į–Ļ–ļ–ł
| –Ď–Ľ–ĺ–ļ
|

|
| K–ĺ—ą–Ķ—Ä
|
|
| –ü–ł—ā–į
|

|
| –õ–ĺ–ī–ļ–į
|

|
–ě—Ā—Ü–ł–Ľ–į—ā–ĺ—Ä–ł
| –ú–ł–≥–į—á (–Ņ–Ķ—Ä–ł–ĺ–ī 2)
|

|
| –Ė–į–Ī–į (–Ņ–Ķ—Ä–ł–ĺ–ī 2)
|

|
| –§–į—Ä (–Ņ–Ķ—Ä–ł–ĺ–ī 2)
|

|
| –ü—É–Ľ—Ā–į—Ä (–Ņ–Ķ—Ä–ł–ĺ–ī 3)
|

|
| –ü–Ķ—ā–Ĺ–į–ī–Ķ—Ā–Ķ—ā–ĺ–Ī–ĺ–Ļ (–Ņ–Ķ—Ä–ł–ĺ–ī 15)
|

|
‚Äě–ü—É–Ľ—Ā–į—Ä—ä—ā‚Äú –Ķ –Ĺ–į–Ļ-—á–Ķ—Ā—ā–ĺ —Ā—Ä–Ķ—Č–į–Ĺ–ł—Ź—ā 3-–Ņ–Ķ—Ä–ł–ĺ–ī–Ķ–Ĺ –ĺ—Ā—Ü–ł–Ľ–į—ā–ĺ—Ä. –ď–ĺ–Ľ—Ź–ľ–ĺ—ā–ĺ –ľ–Ĺ–ĺ–∑–ł–Ĺ—Ā—ā–≤–ĺ –ĺ—ā –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–ĺ –≤—ä–∑–Ĺ–ł–ļ–≤–į—Č–ĺ –ĺ—Ā—Ü–ł–Ľ–į—ā–ĺ—Ä–ł —Ā–į –ī–≤—É–Ņ–Ķ—Ä–ł–ĺ–ī–Ĺ–ł, –ļ–į—ā–ĺ –Ī–Ľ–ł–Ĺ–ļ—ä—Ä –ł –∂–į–Ī–į, –Ĺ–ĺ —Ā–Ķ –∑–Ĺ–į–Ķ, —á–Ķ —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā –ł –ľ–Ĺ–ĺ–≥–ĺ–Ņ–Ķ—Ä–ł–ĺ–ī–Ĺ–ł –ĺ—Ā—Ü–ł–Ľ–į—ā–ĺ—Ä–ł, 4, 8, 14, 15 –ł 30-–Ņ–Ķ—Ä–ł–ĺ–ī–Ĺ–ł –ĺ—Ā—Ü–ł–Ľ–į—ā–ĺ—Ä–ł —Ā–į –Ī–ł–Ľ–ł –ĺ—ā–ļ—Ä–ł–≤–į–Ĺ–ł –ĺ—ā –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–ł –Ĺ–į—á–į–Ľ–Ĺ–ł —É—Ā–Ľ–ĺ–≤–ł—Ź.
–ó–į –ľ–ĺ–ī–Ķ–Ľ–ł, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–ł ‚Äě–ú–į—ā—É—Ā–į–Ľ‚Äú –ĺ—ā–Ĺ–Ķ–ľ–į –ľ–Ĺ–ĺ–≥–ĺ –Ņ–Ķ—Ä–ł–ĺ–ī–ł, –∑–į –ī–į —Ā–Ķ —Ā—ā–į–Ī–ł–Ľ–ł–∑–ł—Ä–į—ā, –ļ–į—ā–ĺ –Ņ—ä—Ä–≤–ł—Ź—ā –ĺ—ā–ļ—Ä–ł—ā ‚Äě–ú–į—ā—É—Ā–į–Ľ‚Äú –Ķ –ł–ľ–Ķ–Ĺ–Ĺ–ĺ R-–Ņ–Ķ–Ĺ—ā–ĺ–ľ–ł–Ĺ–ĺ.
‚Äú–£–ľ–ł—Ä–į–Ļ —ā—Ä—É–ī–Ĺ–ĺ‚Äú –Ķ –ľ–ĺ–ī–Ķ–Ľ, –ļ–ĺ–Ļ—ā–ĺ –≤–Ņ–ĺ—Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ –ł–∑—á–Ķ–∑–≤–į (–≤–ľ–Ķ—Ā—ā–ĺ –ī–į —Ā–Ķ —Ā—ā–į–Ī–ł–Ľ–ł–∑–ł—Ä–į) —Ā–Ľ–Ķ–ī 130 –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł—Ź, –∑–į –ļ–ĺ–Ķ—ā–ĺ —Ā–Ķ —Ā–ľ—Ź—ā–į, —á–Ķ –Ķ –ľ–į–ļ—Ā–ł–ľ—É–ľ—ä—ā –∑–į —Ą–ł–≥—É—Ä–ł —Ā—ä—Ā —Ā–Ķ–ī–Ķ–ľ –ł–Ľ–ł –Ņ–ĺ-–ľ–į–Ľ–ļ–ĺ –ļ–Ľ–Ķ—ā–ļ–ł.
–ó–į ‚Äě–Ė—ä–Ľ—ä–ī‚Äú —Ā–į –Ĺ—É–∂–Ĺ–ł 5206 –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł—Ź –ī–į –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į 633 –ļ–Ľ–Ķ—ā–ļ–ł, –ĺ—ā –ļ–ĺ–ł—ā–ĺ 13 —Ā–į –≥–Ľ–į–Ļ–ī–Ķ—Ä–ł.
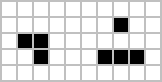
–ď–Ľ–į–Ļ–ī–Ķ—Ä–ł
| –†-–ü–Ķ–Ĺ—ā–ĺ–ľ–ł–Ĺ–ĺ
|

|
| –£–ľ–ł—Ä–į–Ļ —ā—Ä—É–ī–Ĺ–ĺ
|
|
| –Ė—ä–Ľ—ä–ī
|

|
–ö–ĺ–Ĺ—É–Ķ–Ļ –Ņ—ä—Ä–≤–ĺ–Ĺ–į—á–į–Ľ–Ĺ–ĺ –∑–į–ļ–Ľ—é—á–≤–į, —á–Ķ –Ĺ–ł–ļ–ĺ—Ź —Ą–ł–≥—É—Ä–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ä–į—Ā—ā–Ķ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ ‚Äď —Ā –ī—Ä—É–≥–ł –ī—É–ľ–ł, –≤—Ā—Ź–ļ–į –Ĺ–į—á–į–Ľ–Ĺ–į –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł—Ź —Ā –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ –Ī—Ä–ĺ–Ļ –∂–ł–≤–ł –ļ–Ľ–Ķ—ā–ļ–ł, –Ņ–ĺ–Ņ—É–Ľ–į—Ü–ł—Ź—ā–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ņ–ĺ—Ä–į—Ā–Ĺ–Ķ –Ĺ–į–ī –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ –ļ—Ä–į–Ķ–Ĺ –Ī—Ä–ĺ–Ļ. –° –Ņ—ä—Ä–≤–ĺ–Ĺ–į—á–į–Ľ–Ĺ–ĺ—ā–ĺ –ł–∑–Ľ–ł–∑–į–Ĺ–Ķ –Ĺ–į –ł–≥—Ä–į—ā–į –≤ ‚Äě–ú–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ł–≥—Ä–ł‚Äú –ö–ĺ–Ĺ—É–Ķ–Ļ –Ņ—Ä–Ķ–ī–Ľ–į–≥–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā 50 –ī–ĺ–Ľ–į—Ä–į –Ĺ–į –Ņ—ä—Ä–≤–ł—Ź, –ļ–ĺ–Ļ—ā–ĺ —É—Ā–Ņ–Ķ–Ķ –ī–į –ī–ĺ–ļ–į–∂–Ķ –ł–Ľ–ł –ĺ—ā—Ö–≤—ä—Ä–Ľ–ł —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –ľ—É. –Ě–į–≥—Ä–į–ī–į—ā–į –Ķ —Ā–Ņ–Ķ—á–Ķ–Ľ–Ķ–Ĺ–į –Ņ—Ä–Ķ–∑ –Ĺ–ĺ–Ķ–ľ–≤—Ä–ł —Ā—ä—Č–į—ā–į –≥–ĺ–ī–ł–Ĺ–į –ĺ—ā –ĺ—ā–Ī–ĺ—Ä –ĺ—ā MIT, –≤–ĺ–ī–Ķ–Ĺ –ĺ—ā –Ď–ł–Ľ –ď–ĺ—Ā–Ņ—ä—Ä. ‚Äě–ď–Ľ–į–Ļ–ī–Ķ—Ä –ĺ—Ä—ä–ī–ł–Ķ—ā–ĺ –Ĺ–į –ď–ĺ—Ā–Ņ—ä—Ä‚Äú –Ņ—Ä–ĺ–ł–∑–≤–Ķ–∂–ī–į –Ņ—ä—Ä–≤–ł—Ź —Ā–ł –≥–Ľ–į–Ļ–ī–Ķ—Ä –Ĺ–į 15-–ĺ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł–Ķ –ł –Ņ–ĺ –Ķ–ī–ł–Ĺ –≥–Ľ–į–Ļ–ī–Ķ—Ä –Ĺ–į –≤—Ā—Ź–ļ–ĺ 30-–ĺ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–į—ā–į—ā—ä–ļ. –Ē—ä–Ľ–≥–ĺ –≤—Ä–Ķ–ľ–Ķ —ā–ĺ–≤–į –Ķ –Ĺ–į–Ļ-–ľ–į–Ľ–ļ–ł—Ź—ā –Ņ–ĺ–∑–Ĺ–į—ā ‚Äě–≥–Ľ–į–Ļ–ī–Ķ—Ä –ĺ—Ä—ä–ī–ł–Ķ‚Äú (—Ā—ā—Ä—É–ļ—ā—É—Ä–į, –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į—Č–į –≥–Ľ–į–Ļ–ī–Ķ—Ä–ł). –ü—Ä–Ķ–∑ 2015 –Ķ –ĺ—ā–ļ—Ä–ł—ā–ĺ 120-–Ņ–Ķ—Ä–ł–ĺ–ī–Ĺ–ĺ ‚Äě–ĺ—Ä—ä–ī–ł–Ķ‚Äú, –ļ–ĺ–Ķ—ā–ĺ –ł–ľ–į –Ņ–ĺ-–ľ–į–Ľ–ļ–ĺ –∂–ł–≤–ł –ļ–Ľ–Ķ—ā–ļ–ł, –Ĺ–ĺ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ–į –ĺ–≥—Ä–į–Ĺ–ł—á–ł—ā–Ķ–Ľ–Ĺ–į –ļ—É—ā–ł—Ź.
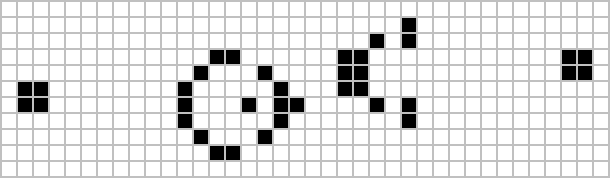
| –ď–Ľ–į–Ļ–ī–Ķ—Ä –ĺ—Ä—ä–ī–ł–Ķ –Ĺ–į –ď–ĺ—Ā–Ņ–Ķ—Ä
|
|
–ü–ĺ-–ļ—ä—Ā–Ĺ–ĺ —Ā–į –ĺ—ā–ļ—Ä–ł—ā–ł –ł –Ņ–ĺ-–ľ–į–Ľ–ļ–ł –ľ–ĺ–ī–Ķ–Ľ–ł, –ļ–ĺ–ł—ā–ĺ —Ā—ä—Č–ĺ –ľ–ĺ–≥–į—ā –ī–į —Ä–į—Ā—ā–į—ā –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ. –í—Ā—Ź–ļ–į –Ķ–ī–Ĺ–į –ĺ—ā —Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ —ā—Ä–ł —Ą–ł–≥—É—Ä–ł —Ä–į—Ā—ā–Ķ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ ‚Äď –Ņ—ä—Ä–≤–ł—ā–Ķ –ī–≤–Ķ —Ā—ä–∑–ī–į–≤–į—ā –Ķ–ī–ł–Ĺ ‚Äě–Ī–Ľ–ĺ–ļ–ĺ–≤ –ī–≤–ł–≥–į—ā–Ķ–Ľ‚Äú, –į —ā—Ä–Ķ—ā–į—ā–į —Ā—ä–∑–ī–į–≤–į –ī–≤–į. –ü—ä—Ä–≤–į—ā–į –ł–ľ–į —Ā–į–ľ–ĺ 10 –∂–ł–≤–ł –ļ–Ľ–Ķ—ā–ļ–ł (–ļ–ĺ–Ķ—ā–ĺ –Ķ –ī–ĺ–ļ–į–∑–į–Ĺ–ĺ, —á–Ķ –Ķ –ľ–ł–Ĺ–ł–ľ—É–ľ—ä—ā). –í—ā–ĺ—Ä–į—ā–į —Ā–Ķ –≤–ľ–Ķ—Ā—ā–≤–į –≤ –ļ–≤–į–ī—Ä–į—ā 5—Ö5. –í–ł—Ā–ĺ—á–ł–Ĺ–į—ā–į –Ĺ–į —ā—Ä–Ķ—ā–į—ā–į –Ķ —Ā–į–ľ–ĺ –Ķ–ī–Ĺ–į –ļ–Ľ–Ķ—ā–ļ–į:



–ü–ĺ-–ļ—ä—Ā–Ĺ–ł –ĺ—ā–ļ—Ä–ł—ā–ł—Ź –≤–ļ–Ľ—é—á–≤–į—ā –ī—Ä—É–≥–ł ‚Äě–ĺ—Ä—ä–ī–ł—Ź‚Äú, –ļ–ĺ–ł—ā–ĺ —Ā–į —Ā—ā–į—Ü–ł–ĺ–Ĺ–į—Ä–Ĺ–ł/–Ĺ–Ķ–Ņ–ĺ–ī–≤–ł–∂–Ĺ–ł –ł –ł–∑—Ā—ā—Ä–Ķ–Ľ–≤–į—ā –≥–Ľ–į–Ļ–ī–Ķ—Ä–ł –ł–Ľ–ł —Ā–ĺ–≤–į–Ľ–ļ–ł. ‚Äě–ü–į—Ä–į—Ö–ĺ–ī—á–Ķ‚Äú –ĺ—Ā—ā–į–≤—Ź —Ā–Ľ–Ķ–ī —Ā–Ķ–Ī–Ķ —Ā–ł –ī–ł—Ä—Ź –ĺ—ā –ĺ—Ā—ā–į—ā—ä—Ü–ł –ł ‚Äě–Ĺ–ĺ—Ā–į—á–ł‚Äú, –ļ–ĺ–ł—ā–ĺ —Ā–Ķ –ī–≤–ł–∂–į—ā –ł –Ņ—Ä–ĺ–ł–∑–≤–Ķ–∂–ī–į—ā —Ā–ĺ–≤–į–Ľ–ļ–ł. –ď–ĺ—Ā–Ņ—ä—Ä —Ā—ä—Č–ĺ —ā–į–ļ–į —Ā—ä–∑–ī–į–≤–į –Ņ—ä—Ä–≤–į—ā–į –ľ–ĺ–∑–į–Ļ–ļ–į —Ā –į—Ā–ł–ľ–Ņ—ā–ĺ—ā–ł—á–Ĺ–ĺ –ĺ–Ņ—ā–ł–ľ–į–Ľ–Ĺ–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–į —Ā–ļ–ĺ—Ä–ĺ—Ā—ā –Ĺ–į —Ä–į—Ā—ā–Ķ–∂, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–į ‚Äě—Ä–į–∑–≤—ä–ī–Ĺ–ł–ļ‚Äú –ł–Ľ–ł ‚Äě–ĺ–ľ–į—Ä‚Äú, –ļ–ĺ—Ź—ā–ĺ —Ä–į–Ī–ĺ—ā–ł, –ļ–į—ā–ĺ –ĺ—Ā—ā–į–≤—Ź —Ā–Ľ–Ķ–ī–į –ĺ—ā –ĺ—Ä—ä–ī–ł—Ź.
–í—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –Ķ –≥–Ľ–į–Ļ–ī–Ķ—Ä–ł—ā–Ķ –ī–į –≤–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–į—ā —Ā –ī—Ä—É–≥–ł –ĺ–Ī–Ķ–ļ—ā–ł –Ņ–ĺ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ–ł –Ĺ–į—á–ł–Ĺ–ł. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –į–ļ–ĺ –ī–≤–į –≥–Ľ–į–Ļ–ī–Ķ—Ä–į —Ā–į –ł–∑—Ā—ā—Ä–Ķ–Ľ—Ź–Ĺ–ł –≤ –Ī–Ľ–ĺ–ļ –Ņ–ĺ —ā–ĺ—á–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ, –Ī–Ľ–ĺ–ļ—ä—ā —Č–Ķ —Ā–Ķ –Ņ—Ä–Ķ–ľ–Ķ—Ā—ā–ł –Ņ–ĺ-–Ī–Ľ–ł–∑–ĺ –ī–ĺ –ł–∑—ā–ĺ—á–Ĺ–ł–ļ–į –Ĺ–į –≥–Ľ–į–Ļ–ī–Ķ—Ä–ł—ā–Ķ. –ź–ļ–ĺ —ā—Ä–ł –≥–Ľ–į–Ļ–ī–Ķ—Ä–į —Ā–į –ł–∑—Ā—ā—Ä–Ķ–Ľ—Ź–Ĺ–ł –Ņ–ĺ —ā–ĺ—á–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ, –Ī–Ľ–ĺ–ļ—ä—ā —Č–Ķ —Ā–Ķ –Ņ—Ä–Ķ–ľ–Ķ—Ā—ā–ł –Ņ–ĺ-–Ĺ–į–ī–į–Ľ–Ķ—á. –Ę–į–∑–ł ‚Äě–Ņ–į–ľ–Ķ—ā‚Äú –Ĺ–į –Ņ–Ľ—ä–∑–≥–į—Č–ł—Ź –Ī–Ľ–ĺ–ļ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į –ļ–į—ā–ĺ —Ā–ł–ľ—É–Ľ–į—Ü–ł—Ź –Ĺ–į –Ī—Ä–ĺ—Ź—á. –í—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –Ķ –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź—ā –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł –ļ–į—ā–ĺ AND, OR –ł NOT –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ļ–ļ–ł –≥–Ľ–į–Ļ–ī–Ķ—Ä–ł. –°—ä—Č–ĺ —ā–į–ļ–į –Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł –ľ–ĺ–∑–į–Ļ–ļ–į, –ļ–ĺ—Ź—ā–ĺ —Ä–į–Ī–ĺ—ā–ł –ļ–į—ā–ĺ –ļ—Ä–į–Ķ–Ĺ –į–≤—ā–ĺ–ľ–į—ā, —Ā–≤—ä—Ä–∑–į–Ĺ —Ā –ī–≤–į –Ī—Ä–ĺ—Ź—á–į. –Ę–ĺ–≤–į –ł–ľ–į —Ā—ä—Č–ł—Ź –Ņ—Ä–ĺ–≥—Ä–į–ľ–Ķ–Ĺ –ļ–į–Ņ–į—Ü–ł—ā–Ķ—ā –ļ–į—ā–ĺ —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ–Ĺ–į—ā–į –ľ–į—ą–ł–Ĺ–į –Ĺ–į –Ę—é—Ä–ł–Ĺ–≥, —ā–ĺ–Ķ—Ā—ā ‚Äě–Ė–ł–≤–ĺ—ā‚Äú –Ķ —ā–Ķ–ĺ—Ä–Ķ—ā–ł—á–Ĺ–ĺ —ā–ĺ–Ľ–ļ–ĺ–≤–į –ľ–ĺ—Č–Ĺ–į, –ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ –≤—Ā–Ķ–ļ–ł –ī—Ä—É–≥ –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä —Ā –Ĺ–Ķ–ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–į –Ņ–į–ľ–Ķ—ā –ł –≤—Ä–Ķ–ľ–Ķ ‚Äď —ā—Ź –Ķ –Ę—é—Ä–ł–Ĺ–≥ –∑–į–≤—ä—Ä—ą–Ķ–Ĺ–į.
–°—ä—Č–ĺ —ā–į–ļ–į, –Ķ–ī–Ĺ–į –ľ–ĺ–∑–į–Ļ–ļ–į –ľ–ĺ–∂–Ķ –ī–į —Ā—ä–ī—ä—Ä–∂–į –Ĺ–į–Ī–ĺ—Ä –ĺ—ā –ĺ—Ä—ä–ī–ł—Ź, –ļ–ĺ–ł—ā–ĺ –ł–∑—Ā—ā—Ä–Ķ–Ľ–≤–į—ā –≥–Ľ–į–Ļ–ī–Ķ—Ä–ł –Ņ–ĺ —ā–į–ļ—ä–≤ –Ĺ–į—á–ł–Ĺ, —á–Ķ –ī–į –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į—ā –Ĺ–ĺ–≤–ł –ĺ–Ī–Ķ–ļ—ā–ł, –≤–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ĺ–ĺ –ļ–ĺ–Ņ–ł—Ź –Ĺ–į –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–Ĺ–į—ā–į —Ą–ł–≥—É—Ä–į. –ú–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ–Ķ–Ĺ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–ĺ—Ä, –≤ –ļ–ĺ–Ļ—ā–ĺ –ī–į –Ķ –≤–ļ–Ľ—é—á–Ķ–Ĺ –Ę—é—Ä–ł–Ĺ–≥ –∑–į–≤—ä—Ä—ą–Ķ–Ĺ –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä –ł –ļ–ĺ–Ļ—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į —Ā—ā—Ä–ĺ–ł –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –≤–ł–ī–ĺ–≤–Ķ —Ā–Ľ–ĺ–∂–Ĺ–ł –ĺ–Ī–Ķ–ļ—ā–ł, –≤–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ĺ–ĺ –ł –ļ–ĺ–Ņ–ł—Ź –Ĺ–į —Ā–Ķ–Ī–Ķ —Ā–ł.
–°–į–ľ–ĺ–≤—ä–∑–Ņ—Ä–ĺ–ł–∑–≤–Ķ–∂–ī–į–Ĺ–Ķ
–Ě–į 18 –ľ–į–Ļ 2010 –ź–Ĺ–ī—Ä—é –£–Ķ–Ļ–ī –ĺ–Ī—Ź–≤–ł —Ā–į–ľ–ĺ–Ņ–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į—Č–į —Ā–Ķ –ľ–ĺ–∑–į–Ļ–ļ–į, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–į –Ď–Ľ–ł–∑–Ĺ–į—Ü–ł (Gemini), –ļ–ĺ—Ź—ā–ĺ —Ā—ä–∑–ī–į–≤–į –ļ–ĺ–Ņ–ł—Ź –Ĺ–į —Ā–Ķ–Ī–Ķ —Ā–ł –ł —É–Ĺ–ł—Č–ĺ–∂–į–≤–į –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–į. –Ę–į–∑–ł –ľ–ĺ–∑–į–Ļ–ļ–į —Ā–Ķ –≤—ä–∑–Ņ—Ä–ĺ–ł–∑–≤–Ķ–∂–ī–į –≤ 34 –ľ–ł–Ľ–ł–ĺ–Ĺ–į –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł—Ź –ł –ł–∑–Ņ–ĺ–Ľ–∑–≤–į –Ĺ–į—Ä—ä—á–Ĺ–ł–ļ, –Ĺ–į–Ņ—Ä–į–≤–Ķ–Ĺ –ĺ—ā –≥–Ľ–į–Ļ–ī–Ķ—Ä–ł, –ļ–ĺ–ł—ā–ĺ –ĺ—Ā—Ü–ł–Ľ–ł—Ä–į—ā –ľ–Ķ–∂–ī—É –ī–≤–Ķ —Ā—ā–į–Ī–ł–Ľ–Ĺ–ł –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ł, –Ĺ–į–Ņ—Ä–į–≤–Ķ–Ĺ–ł –ĺ—ā –ß–į–Ņ–ľ—ä–Ĺ-–ď—Ä–ł–Ļ–Ĺ —Ā—ā—Ä–ĺ–ł—ā–Ķ–Ľ–Ĺ–ł —Ä—ä—Ü–Ķ. –Ę–Ķ–∑–ł –Ĺ–į —Ā–≤–ĺ–Ļ —Ä–Ķ–ī —Ā—ä–∑–ī–į–≤–į—ā –ļ–ĺ–Ņ–ł—Ź –Ĺ–į –ľ–ĺ–∑–į–Ļ–ļ–į—ā–į –ł —É–Ĺ–ł—Č–ĺ–∂–į–≤–į—ā –Ņ—Ä–Ķ–ī–ł—ą–Ĺ–ĺ—ā–ĺ –ļ–ĺ–Ņ–ł–Ķ. Gemini –Ķ —Ā—ä—Č–ĺ —ā–į–ļ–į –ł —Ā–ĺ–≤–į–Ľ–ļ–į, –ļ–ĺ—Ź—ā–ĺ –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā –Ĺ–Ķ –Ķ –Ĺ–ł—ā–ĺ –ĺ—Ä—ā–ĺ–≥–ĺ–Ĺ–į–Ľ–Ĺ–į, –Ĺ–ł—ā–ĺ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–Ĺ–į (—ā–Ķ–∑–ł —Ā–į –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–ł –ļ–ĺ–Ĺ–Ĺ–ł—Ü–ł).
–Ě–į 23 –Ĺ–ĺ–Ķ–ľ–≤—Ä–ł 2013 –Ē–Ķ–Ļ–≤ –ď—Ä–ł–Ļ–Ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į –Ņ—ä—Ä–≤–ł—Ź —Ä–Ķ–Ņ–Ľ–ł–ļ–į—ā–ĺ—Ä –≤ ‚Äě–Ė–ł–≤–ĺ—ā‚Äú, –ļ–ĺ–Ļ—ā–ĺ —Ā—ä–∑–ī–į–≤–į –∑–į–≤—ä—Ä—ą–Ķ–Ĺ–ĺ –ļ–ĺ–Ņ–ł–Ķ –Ĺ–į —Ā–Ķ–Ī–Ķ —Ā–ł, –≤–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ĺ–ĺ –ł –Ĺ–į—Ä—ä—á–Ĺ–ł–ļ–į.
–ė—ā–Ķ—Ä–į—Ü–ł—Ź
–ě—ā –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–į –Ĺ–į—á–į–Ľ–Ĺ–į –ľ–ĺ–∑–į–Ļ–ļ–į –ĺ—ā –∂–ł–≤–ł –ļ–Ľ–Ķ—ā–ļ–ł –Ĺ–į –Ņ–ĺ–Ľ–Ķ—ā–ĺ, –Ĺ–į–Ī–Ľ—é–ī–į—ā–Ķ–Ľ–ł—ā–Ķ —Č–Ķ –≤–ł–ī—Ź—ā –ļ–į–ļ –Ņ–ĺ–Ņ—É–Ľ–į—Ü–ł—Ź—ā–į —Ā–Ķ —Ā–ľ–Ķ–Ĺ—Ź –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł–Ķ —Ā–Ľ–Ķ–ī –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł–Ķ. –ú–ĺ–∑–į–Ļ–ļ–ł—ā–Ķ, –ļ–ĺ–ł—ā–ĺ —Ā–Ķ –ĺ–Ī—Ä–į–∑—É–≤–į –ĺ—ā –Ņ—Ä–ĺ—Ā—ā–ł—ā–Ķ –Ņ—Ä–į–≤–ł–Ľ–į, –ľ–ĺ–≥–į—ā –ī–į –Ī—ä–ī–į—ā —Ä–į–∑–≥–Ľ–Ķ–ī–į–Ĺ–ł –ļ–į—ā–ĺ —Ą–ĺ—Ä–ľ–į –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į –ļ—Ä–į—Ā–ĺ—ā–į. –ú–į–Ľ–ļ–ł –ł–∑–ĺ–Ľ–ł—Ä–į–Ĺ–ł –Ņ–ĺ–ī–ľ–ĺ–∑–į–Ļ–ļ–ł –Ī–Ķ–∑ –Ĺ–į—á–į–Ľ–Ĺ–į —Ā–ł–ľ–Ķ—ā—Ä–ł—Ź –ł–ľ–į—ā —Ā–ļ–Ľ–ĺ–Ĺ–Ĺ–ĺ—Ā—ā—ā–į –ī–į —Ā–Ķ –Ņ—Ä–Ķ–≤—Ä—ä—Č–į—ā –≤ —Ā–ł–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł. –í–Ķ–ī–Ĺ—ä–∂ —Ā–Ľ—É—á–ł–Ľ–ĺ —Ā–Ķ, —Ā–ł–ľ–Ķ—ā—Ä–ł—Ź—ā–į –ľ–ĺ–∂–Ķ –ī–į —Ā—ā–į–Ĺ–Ķ –Ņ–ĺ-–Ī–ĺ–≥–į—ā–į, –Ĺ–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ł–∑–≥—É–Ī–Ķ–Ĺ–į –ĺ—Ā–≤–Ķ–Ĺ –į–ļ–ĺ —Ā—ä—Ā–Ķ–ī–Ĺ–į –Ņ–ĺ–ī–ľ–ĺ–∑–į–Ļ–ļ–į –Ĺ–Ķ —Ā–Ķ –Ņ—Ä–ł–Ī–Ľ–ł–∂–ł –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ĺ –Ī–Ľ–ł–∑–ļ–ĺ, –∑–į –ī–į —Ź —Ä–į–∑—Ä—É—ą–ł. –í –ľ–Ĺ–ĺ–≥–ĺ –ľ–į–Ľ—ä–ļ –Ī—Ä–ĺ–Ļ —Ā–Ľ—É—á–į–ł –ĺ–Ī—Č–Ķ—Ā—ā–≤–ĺ—ā–ĺ —É–ľ–ł—Ä–į –ł–∑—Ü—Ź–Ľ–ĺ, –Ĺ–ĺ —ā–ĺ–≤–į —Ā–Ķ —Ā–Ľ—É—á–≤–į —Ā–Ľ–Ķ–ī –≥–ĺ–Ľ—Ź–ľ–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł—Ź. –ü–ĺ–≤–Ķ—á–Ķ—ā–ĺ –Ĺ–į—á–į–Ľ–Ĺ–ł –ľ–ĺ–∑–į–Ļ–ļ–ł ‚Äě–ł–∑–≥–į—Ä—Ź—ā‚Äú –≤ –Ķ–ī–ł–Ĺ –ľ–ĺ–ľ–Ķ–Ĺ—ā, –ĺ—Ā—ā–į–≤—Ź–Ļ–ļ–ł —Ā—ā–į–Ī–ł–Ľ–Ĺ–ł —Ą–ł–≥—É—Ä–ł –ł–Ľ–ł –ľ–ĺ–∑–į–Ļ–ļ–ł, –ļ–ĺ–ł—ā–ĺ –ĺ—Ā—Ü–ł–Ľ–ł—Ä–į—ā –ľ–Ķ–∂–ī—É –ī–≤–Ķ –ł–Ľ–ł –Ņ–ĺ–≤–Ķ—á–Ķ —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł—Ź. –ú–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ —Ā—ä—Č–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–∂–ī–į—ā –Ķ–ī–ł–Ĺ –ł–Ľ–ł –Ņ–ĺ–≤–Ķ—á–Ķ –≥–Ľ–į–Ļ–ī–Ķ—Ä–į –ł–Ľ–ł —Ā–ĺ–≤–į–Ľ–ļ–ł, –ļ–ĺ–ł—ā–ĺ –Ņ—ä—ā—É–≤–į—ā –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ –Ĺ–į–ī–į–Ľ–Ķ—á –ĺ—ā –Ĺ–į—á–į–Ľ–Ĺ–į—ā–į —ā–ĺ—á–ļ–į. –ó–į—Ä–į–ī–ł –Ņ—Ä–į–≤–ł–Ľ–į—ā–į, –Ī–į–∑–ł—Ä–į–Ĺ–ł –Ĺ–į —Ā—ä—Ā–Ķ–ī—Ā—ā–≤–ĺ, –Ĺ–ł–ļ–į–ļ–≤–į –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ņ—ä—ā—É–≤–į –Ņ–ĺ –Ņ–ĺ–Ľ–Ķ—ā–ĺ —Ā –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ–į —Ā–ļ–ĺ—Ä–ĺ—Ā—ā –ĺ—ā –Ķ–ī–Ĺ–į –ļ–Ľ–Ķ—ā–ļ–į –Ĺ–į –Ņ–Ķ—Ä–ł–ĺ–ī –∑–į—ā–ĺ–≤–į –ł —ā–į–∑–ł —Ā–ļ–ĺ—Ä–ĺ—Ā—ā –Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–į –ļ–į—ā–ĺ —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—ā–į –Ĺ–į —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–į—ā–į –≤ –ļ–Ľ–Ķ—ā—ä—á–Ĺ–ł—ā–Ķ –į–≤—ā–ĺ–ľ–į—ā–ł –ł —Ā–Ķ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–≤–į —Ā C.
–ź–Ľ–≥–ĺ—Ä–ł—ā–ľ–ł
–†–į–Ĺ–Ĺ–ł—ā–Ķ —Ą–ĺ—Ä–ľ–ł —Ā –Ĺ–Ķ–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ĺ —Ä–į–∑–≤–ł—ā–ł–Ķ, –ļ–į—ā–ĺ –†-–Ņ–Ķ–Ĺ—ā–ĺ–ľ–ł–Ĺ–ĺ, –Ņ–ĺ–ī—ā–ł–ļ–Ĺ–į–Ľ–ł –Ņ—Ä–ĺ–≥—Ä–į–ľ–ł—Ā—ā–ł—ā–Ķ –Ņ–ĺ —Ā–≤–Ķ—ā–į –ī–į –Ņ–ł—ą–į—ā –Ņ—Ä–ĺ–≥—Ä–į–ľ–ł, —Ā –ļ–ĺ–ł—ā–ĺ –ī–į –Ņ—Ä–ĺ—Ā–Ľ–Ķ–ī—Ź—ā —Ä–į–∑–≤–ł—ā–ł–Ķ—ā–ĺ –Ĺ–į —Ą–ĺ—Ä–ľ–ł—ā–Ķ –ĺ—ā –ł–≥—Ä–į—ā–į. –ü–ĺ–≤–Ķ—á–Ķ—ā–ĺ —Ä–į–Ĺ–Ĺ–ł –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ł –Ī–ł–Ľ–ł –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł: –ļ–Ľ–Ķ—ā–ļ–ł—ā–Ķ —Ā–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ź–Ľ–ł –ļ–į—ā–ĺ –ī–≤—É–ł–∑–ľ–Ķ—Ä–Ķ–Ĺ –ľ–į—Ā–ł–≤ –≤ –Ņ–į–ľ–Ķ—ā—ā–į –Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–į. –Ě–į–Ļ-—á–Ķ—Ā—ā–ĺ —Ā–Ķ –Ņ–ĺ–Ľ–∑–≤–į—ā –ī–≤–į –ľ–į—Ā–ł–≤–į: –Ņ—ä—Ä–≤–ł—Ź—ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –ĺ—ā –ļ–Ľ–Ķ—ā–ļ–ł –ĺ—ā —ā–Ķ–ļ—É—Č–ĺ—ā–ĺ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł–Ķ, –į –≤—ä–≤ –≤—ā–ĺ—Ä–ł—Ź —Ā–Ķ –ł–∑—á–ł—Ā–Ľ—Ź–≤–į –ł –∑–į–Ņ–ł—Ā–≤–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –ĺ—ā –ļ–Ľ–Ķ—ā–ļ–ł –ĺ—ā —Ā–Ľ–Ķ–ī–≤–į—Č–ĺ—ā–ĺ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł–Ķ. –ě–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ĺ –∑–į –ĺ–Ņ–ł—Ā–į–Ĺ–ł–Ķ –Ĺ–į —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–į—ā–į –ļ–Ľ–Ķ—ā–ļ–į ‚Äď –∂–ł–≤–į –ł–Ľ–ł –ľ—ä—Ä—ā–≤–į —Ā–Ķ –Ņ–ĺ–Ľ–∑–≤–į—ā —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–ĺ 1 –ł–Ľ–ł 0. –ó–į –ĺ–Ī—Ö–ĺ–∂–ī–į–Ĺ–Ķ –Ĺ–į –ľ–į—Ā–ł–≤–į –ł –∑–į –ł–∑—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź—ā–į —Ā–Ķ –ł–ľ–Ņ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł—Ä–į—ā –≤–Ľ–ĺ–∂–Ķ–Ĺ–ł —Ü–ł–ļ–Ľ–ł, –ļ–į—ā–ĺ —Ā–Ķ –ł—ā–Ķ—Ä–ł—Ä–į –Ņ—Ä–Ķ–∑ –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł—ā–Ķ –ł –∑–į –≤—Ā–Ķ–ļ–ł –Ķ–ī–ł–Ĺ –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā —Ā–Ķ –ł—ā–Ķ—Ä–ł—Ä–į –Ņ—Ä–Ķ–∑ —Ā—ä—Ā–Ķ–ī–Ĺ–ł—ā–Ķ –ľ—É, –Ņ—Ä–Ķ–Ī—Ä–ĺ—Ź–≤–į–Ļ–ļ–ł –ĺ–Ĺ–Ķ–∑–ł, –ļ–ĺ–ł—ā–ĺ —Ā–į –∂–ł–≤–ł, –ļ–į—ā–ĺ –ĺ—ā —Ä–Ķ–∑—É–Ľ—ā–į—ā–į –ĺ—ā –Ņ—Ä–Ķ–Ī—Ä–ĺ—Ź–≤–į–Ĺ–Ķ—ā–ĺ —Ā–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź –ī–į–Ľ–ł —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–į—ā–į –ļ–Ľ–Ķ—ā–ļ–į –Ķ –∂–ł–≤–į –ł–Ľ–ł –ľ—ä—Ä—ā–≤–į. –†–Ķ–∑—É–Ľ—ā–į—ā—ä—ā —Ā–Ķ –∑–į–Ņ–ł—Ā–≤–į –≤ —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–į—ā–į –ļ–Ľ–Ķ—ā–ļ–į –Ĺ–į –≤—ā–ĺ—Ä–ł—Ź –ľ–į—Ā–ł–≤. –ú–į—Ā–ł–≤—ä—ā —Ā–Ķ –ł–∑–ĺ–Ī—Ä–į–∑—Ź–≤–į –Ĺ–į –Ķ–ļ—Ä–į–Ĺ–į. –°–Ľ–Ķ–ī –ļ–į—ā–ĺ –ĺ–Ī—Ö–ĺ–∂–ī–į–Ĺ–Ķ—ā–ĺ –Ņ—Ä–ł–ļ–Ľ—é—á–ł, –ľ–į—Ā–ł–≤–ł—ā–Ķ —Ā–Ķ —Ä–į–∑–ľ–Ķ–Ĺ—Ź—ā, –ļ–į—ā–ĺ –ľ–į—Ā–ł–≤—ä—ā ‚Äď –Ĺ–į—Ā–Ľ–Ķ–ī–Ĺ–ł–ļ –ĺ—ā –Ņ—Ä–Ķ–ī–ł—ą–Ĺ–į—ā–į –ł—ā–Ķ—Ä–į—Ü–ł—Ź –≤–Ķ—á–Ķ —Ā–Ķ —ā—Ä–Ķ—ā–ł—Ä–į –ļ–į—ā–ĺ –Ĺ–į—Ā—ā–ĺ—Ź—Č.
–°—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā –ľ–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–Ĺ–ł –Ľ–Ķ–ļ–ł –Ņ–ĺ–ī–ĺ–Ī—Ä–Ķ–Ĺ–ł—Ź, –ļ–ĺ–ł—ā–ĺ –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –Ņ—Ä–ł–Ľ–ĺ–∂–į—ā –ļ—ä–ľ —ā–į–∑–ł –ĺ–Ī—Č–į —Ā—Ö–Ķ–ľ–į, –ļ–ĺ–ł—ā–ĺ —Ā–Ņ–ĺ–ľ–į–≥–į—ā –∑–į —Ä–Ķ–ī—É—Ü–ł—Ä–į–Ĺ–Ķ –Ĺ–į –Ĺ—Ź–ļ–ĺ–ł –ł–∑–Ľ–ł—ą–Ĺ–ł –ł–∑—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –į–ļ–ĺ —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –∑–ĺ–Ĺ–į –ĺ—ā –ľ–į—Ā–ł–≤–į (–ī–į–ī–Ķ–Ĺ–į –ļ–Ľ–Ķ—ā–ļ–į —Ā –≤—Ā–ł—á–ļ–ł—ā–Ķ —Ě —Ā—ä—Ā–Ķ–ī–Ĺ–ł –ļ–Ľ–Ķ—ā–ļ–ł), –≤ –ļ–ĺ—Ź—ā–ĺ –Ĺ–Ķ —Ā–į –Ĺ–į—Ā—ā—ä–Ņ–ł–Ľ–ł –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ł –≤ —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł—Ź—ā–į –Ĺ–į –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł—ā–Ķ –Ņ–ĺ –≤—Ä–Ķ–ľ–Ķ –Ĺ–į —ā–Ķ–ļ—É—Č–į—ā–į –ł—ā–Ķ—Ä–į—Ü–ł—Ź, —ā–ĺ —Ā—ä—Ā —Ā–ł–≥—É—Ä–Ĺ–ĺ—Ā—ā –Ĺ—Ź–ľ–į –ī–į –Ĺ–į—Ā—ā—ä–Ņ—Ź—ā –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ł –ł –≤ —Ā–Ľ–Ķ–ī–≤–į—Č–į—ā–į. –ü–ĺ —ā–ĺ–∑–ł –Ĺ–į—á–ł–Ĺ –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ —Ā–Ľ–Ķ–ī—Ź—ā —Ā–į–ľ–ĺ –į–ļ—ā–ł–≤–Ĺ–ł—ā–Ķ –∑–ĺ–Ĺ–ł –ł –ī–į —Ā–Ķ –Ņ—Ä–ĺ–Ņ—É—Ā–Ĺ–Ķ –ĺ–Ī—Ö–ĺ–∂–ī–į–Ĺ–Ķ –ł –į–ļ—ā—É–į–Ľ–ł–∑–į—Ü–ł—Ź –Ĺ–į –Ĺ–Ķ–į–ļ—ā–ł–≤–Ĺ–ł—ā–Ķ.
–ó–į –ī–į —Ā–Ķ –ł–∑–Ī–Ķ–≥–Ĺ–į—ā —Ä–į–∑–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź –Ĺ–į –Ņ—Ä–ĺ—Ü–Ķ—Ā–į –Ņ–ĺ –≤—Ä–Ķ–ľ–Ķ –Ĺ–į –ĺ–Ī—Ö–ĺ–∂–ī–į–Ĺ–Ķ—ā–ĺ –≤—ä–≤ –≤—ä—ā—Ä–Ķ—ą–Ĺ–ł—Ź —Ü–ł–ļ—ä–Ľ, –ľ–ĺ–∂–Ķ–ľ –ī–į –Ņ—Ä–ł–Ī–Ķ–≥–Ĺ–Ķ–ľ –ĺ—ā –Ķ–≥–ĺ—Ü–Ķ–Ĺ—ā—Ä–ł—á–Ĺ–į –Ņ–Ķ—Ä—Ā–Ņ–Ķ–ļ—ā–ł–≤–į, –ļ—ä–ī–Ķ—ā–ĺ —Ā–Ķ —Ä–į–∑–≥–Ľ–Ķ–∂–ī–į—ā –ĺ—ā–ī–Ķ–Ľ–Ĺ–ł—ā–Ķ –≤–∑–į–ł–ľ–ĺ–≤—Ä—ä–∑–ļ–ł –ľ–Ķ–∂–ī—É —Ü–Ķ–Ĺ—ā—Ä–į–Ľ–Ĺ–į—ā–į –ļ–Ľ–Ķ—ā–ļ–į –ł –Ĺ–Ķ–Ļ–Ĺ–ł—ā–Ķ —Ā—ä—Ā–Ķ–ī–ł –ļ—ä–ľ –Ņ–ĺ-–ĺ–Ī—Č–į—ā–į –Ņ–Ķ—Ä—Ā–Ņ–Ķ–ļ—ā–ł–≤–į –Ĺ–į ‚Äě–Ĺ–į—É—á–Ĺ–ĺ –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł–Ķ‚Äú: –į–ļ–ĺ —Ā—É–ľ–į—ā–į –Ĺ–į –≤—Ā–ł—á–ļ–ł 9 –ļ–Ľ–Ķ—ā–ļ–ł –Ķ —Ä–į–≤–Ĺ–į –Ĺ–į 3, —ā–ĺ —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —Ü–Ķ–Ĺ—ā—Ä–į–Ľ–Ĺ–į—ā–į –ļ–Ľ–Ķ—ā–ļ–į –≤ —Ā–Ľ–Ķ–ī–≤–į—Č–ĺ—ā–ĺ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł–Ķ —Č–Ķ –Ķ ‚Äě–∂–ł–≤–ĺ—ā‚Äú (1), –Ī–Ķ–∑ –ī–į —Ā–Ķ –≤–∑–ł–ľ–į –Ņ—Ä–Ķ–ī–≤–ł–ī –ľ–ĺ–ľ–Ķ–Ĺ—ā–Ĺ–ĺ—ā–ĺ —Ě —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ. –ź–ļ–ĺ —Ā—É–ľ–į—ā–į –Ķ —Ä–į–≤–Ĺ–į –Ĺ–į 4, –ļ–Ľ–Ķ—ā–ļ–į—ā–į –Ĺ–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ —Ā–ł. –ü—Ä–ł –≤—Ā—Ź–ļ–į –ī—Ä—É–≥–į —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā –Ĺ–į —Ā—É–ľ–į—ā–į, —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ —Ě —Ā—ā–į–≤–į ‚Äě—Ā–ľ—ä—Ä—ā‚Äú (0).
–ü—Ä–ł –Ĺ—É–∂–ī–į –ĺ—ā –Ņ–Ķ—Ā—ā–Ķ–Ĺ–Ķ –Ĺ–į –Ņ–į–ľ–Ķ—ā, –≤—ā–ĺ—Ä–ł—Ź—ā –ī–≤—É–ľ–Ķ—Ä–Ķ–Ĺ –ľ–į—Ā–ł–≤ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –∑–į–ľ–Ķ–Ĺ–Ķ–Ĺ —Ā 3 –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ł –Ķ–ī–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ł –Ī—É—Ą–Ķ—Ä–Ĺ–ł –ľ–į—Ā–ł–≤–į ‚Äď –≤ –Ņ—ä—Ä–≤–ł—Ź –Ī—É—Ą–Ķ—Ä —Ā–Ķ –∑–į–Ņ–ł—Ā–≤–į —Ä–Ķ–∑—É–Ľ—ā–į—ā–į –ĺ—ā –ł–∑—á–ł—Ā–Ľ–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –Ķ–ī–ł–Ĺ —Ä–Ķ–ī –ĺ—ā –ī–≤—É–ľ–Ķ—Ä–Ĺ–ł—Ź –ľ–į—Ā–ł–≤, —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į –≤—ä–≤ –≤—ā–ĺ—Ä–ł—Ź –Ī—É—Ą–Ķ—Ä —Ā–Ķ –∑–į–Ņ–ł—Ā–≤–į —Ä–Ķ–∑—É–Ľ—ā–į—ā–į –ĺ—ā –ł–∑—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź—ā–į –Ĺ–į —Ā–Ľ–Ķ–ī–≤–į—Č–ł—Ź —Ä–Ķ–ī, –ļ–į—ā–ĺ –Ĺ–į –Ņ—Ä–Ķ–ī—Ö–ĺ–ī–Ĺ–ł—Ź —Ä–Ķ–ī —Ā–Ķ –Ņ—Ä–Ķ–∑–į–Ņ–ł—Ā–≤–į —Ā—ä–ī—ä—Ä–∂–į–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –Ņ—ä—Ä–≤–ł—Ź –Ī—É—Ą–Ķ—Ä, –ļ–ĺ–Ļ—ā–ĺ –≤–Ķ—á–Ķ –Ķ —Ā–≤–ĺ–Ī–ĺ–ī–Ķ–Ĺ –ī–į –Ņ—Ä–ł–Ķ–ľ–Ķ —Ä–Ķ–∑—É–Ľ—ā–į—ā–ł—ā–Ķ –ĺ—ā –ł–∑—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź—ā–į –Ĺ–į —ā—Ä–Ķ—ā–ł—Ź —Ä–Ķ–ī –ĺ—ā –ľ–į—Ā–ł–≤–į –ł —ā.–Ĺ. –ī–ĺ –ļ—Ä–į—Ź. –í —Ā–Ľ—É—á–į–Ļ, —á–Ķ —Ā–Ķ –Ņ–ĺ–Ľ–∑–≤–į —ā–ĺ—Ä–ĺ–ł–ī–į–Ľ–Ķ–Ĺ –ľ–į—Ā–ł–≤, –Ķ –Ĺ—É–∂–Ķ–Ĺ –ł —ā—Ä–Ķ—ā–ł –Ī—É—Ą–Ķ—Ä, –ļ–ĺ–Ļ—ā–ĺ –ī–į –Ņ–į–∑–ł –Ĺ–į—á–į–Ľ–Ĺ–ĺ—ā–ĺ —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –Ĺ–į –Ņ—ä—Ä–≤–ł—Ź —Ä–Ķ–ī, –ī–ĺ–ļ–į—ā–ĺ –Ĺ–Ķ —Ā–Ķ –ł–∑—á–ł—Ā–Ľ–ł –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł—Ź —Ä–Ķ–ī.
 –°–Ĺ–ł–ľ–ļ–į –Ĺ–į puffer-type breeder (—á–Ķ—Ä–≤–Ķ–Ĺ–ł), –ļ–ĺ–Ļ—ā–ĺ –ĺ—Ā—ā–į–≤—Ź –≥–Ľ–į–Ļ–ī–Ķ—Ä –ĺ—Ä—ä–∂–ł—Ź (–∑–Ķ–Ľ–Ķ–Ĺ–ł) –Ņ–ĺ –Ņ—ä—ā—Ź —Ā–ł, –ļ–ĺ–ł—ā–ĺ –Ĺ–į —Ā–≤–ĺ–Ļ —Ä–Ķ–ī —Ā—ä–∑–ī–į–≤–į—ā –≥–Ľ–į–Ļ–ī–Ķ—Ä–ł (—Ā–ł–Ĺ–ł)
–°–Ĺ–ł–ľ–ļ–į –Ĺ–į puffer-type breeder (—á–Ķ—Ä–≤–Ķ–Ĺ–ł), –ļ–ĺ–Ļ—ā–ĺ –ĺ—Ā—ā–į–≤—Ź –≥–Ľ–į–Ļ–ī–Ķ—Ä –ĺ—Ä—ä–∂–ł—Ź (–∑–Ķ–Ľ–Ķ–Ĺ–ł) –Ņ–ĺ –Ņ—ä—ā—Ź —Ā–ł, –ļ–ĺ–ł—ā–ĺ –Ĺ–į —Ā–≤–ĺ–Ļ —Ä–Ķ–ī —Ā—ä–∑–ī–į–≤–į—ā –≥–Ľ–į–Ļ–ī–Ķ—Ä–ł (—Ā–ł–Ĺ–ł)
–ü–ĺ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –Ņ–ĺ–Ľ–Ķ—ā–ĺ, –≤—ä—Ä—Ö—É –ļ–ĺ–Ķ—ā–ĺ —Ā–Ķ —Ä–į–∑–Ņ—Ä–ĺ—Ā—ā–ł—Ä–į –ł–≥—Ä–į—ā–į ‚Äě–Ė–ł–≤–ĺ—ā‚Äú, –Ķ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ, –Ĺ–ĺ –ļ–ĺ–ľ–Ņ—é—ā—Ä–ł—ā–Ķ –ł–ľ–į—ā –ļ—Ä–į–Ļ–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –Ņ–į–ľ–Ķ—ā. –Ę–ĺ–≤–į –ľ–ĺ–∂–Ķ –ī–į –Ņ–ĺ—Ä–ĺ–ī–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ, –ļ–ĺ–≥–į—ā–ĺ —Ā–Ķ –ł—ā–Ķ—Ä–ł—Ä–į –ĺ–ļ–ĺ–Ľ–ĺ –≥—Ä–į–Ĺ–ł—Ü–ł—ā–Ķ –Ĺ–į –ľ–į—Ā–ł–≤–į. –ü—Ä–ĺ–≥—Ä–į–ľ–ł—Ā—ā–ł—ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ —Ā—ā—Ä–į—ā–Ķ–≥–ł–ł –∑–į —Ā–Ņ—Ä–į–≤—Ź–Ĺ–Ķ —Ā —ā–ĺ–∑–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ. –Ě–į–Ļ-–Ņ—Ä–ĺ—Ā—ā–į—ā–į —Ā—ā—Ä–į—ā–Ķ–≥–ł—Ź –Ķ –ī–į —Ā–Ķ –ī–ĺ–Ņ—É—Ā–Ĺ–Ķ, —á–Ķ –ļ–Ľ–Ķ—ā–ļ–ł—ā–Ķ –ł–∑–≤—ä–Ĺ –ľ–į—Ā–ł–≤–į —Ā–į –ľ—ä—Ä—ā–≤–ł (0). –Ę–ĺ–∑–ł –Ņ–ĺ–ī—Ö–ĺ–ī —Ā–Ķ –ł–ľ–Ņ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł—Ä–į –Ľ–Ķ—Ā–Ĺ–ĺ, –Ĺ–ĺ –≤–ĺ–ī–ł –ī–ĺ –Ĺ–Ķ–Ņ—Ä–į–≤–ł–Ľ–Ĺ–ł —Ä–Ķ–∑—É–Ľ—ā–į—ā–ł, –ļ–ĺ–≥–į—ā–ĺ –į–ļ—ā–ł–≤–Ĺ–į—ā–į –∑–ĺ–Ĺ–į –Ņ—Ä–Ķ—Ā–Ķ—á–Ķ –≥—Ä–į–Ĺ–ł—Ü–į –Ĺ–į –ľ–į—Ā–ł–≤–į. –ü–ĺ-—Ā–Ľ–ĺ–∂–Ĺ–ł—Ź –Ņ–ĺ–ī—Ö–ĺ–ī –Ķ –ī–į –ļ—Ä–į–ł—Č–į—ā–į –Ĺ–į –ľ–į—Ā–ł–≤–į –ī–į —Ā–Ķ —Ā—á–ł—ā–į—ā –∑–į —Ā—ä—Ā–Ķ–ī–Ĺ–ł ‚Äď –Ľ–Ķ–≤–ł—Ź –ł –ī–Ķ—Ā–Ĺ–ł—Ź –ĺ—ā –Ķ–ī–Ĺ–į —Ā—ā—Ä–į–Ĺ–į –ł –≥–ĺ—Ä–Ĺ–ł—Ź –ł –ī–ĺ–Ľ–Ĺ–ł—Ź –ĺ—ā –ī—Ä—É–≥–į, –ļ–ĺ–Ķ—ā–ĺ –ĺ–Ī—É—Ā–Ľ–į–≤—Ź –ľ–į—Ā–ł–≤ —Ā —ā–ĺ—Ä–ĺ–ł–ī–į–Ľ–Ĺ–į —Ą–ĺ—Ä–ľ–į. –í —Ä–Ķ–∑—É–Ľ—ā–į—ā –Ĺ–į —ā–ĺ–≤–į, –ļ–ĺ–≥–į—ā–ĺ –į–ļ—ā–ł–≤–Ĺ–į—ā–į –ĺ–Ī–Ľ–į—Ā—ā –Ņ—Ä–Ķ–ľ–ł–Ĺ–Ķ –ī–į –ļ–į–∂–Ķ–ľ –ī–ĺ–Ľ–Ĺ–ł—Ź (–ī–Ķ—Ā–Ĺ–ł—Ź) –ļ—Ä–į–Ļ, —ā—Ź —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź–≤–į –≤ –≥–ĺ—Ä–Ĺ–ł—Ź (–Ľ–Ķ–≤–ł—Ź) –ļ—Ä–į–Ļ. –ė –Ņ—Ä–ł —ā–ĺ–∑–ł —Ā—ā—Ä–į—ā–Ķ–≥–ł—Ź –Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–į –Ņ–ĺ—Ź–≤–į—ā–į –Ĺ–į –Ĺ—Ź–ļ–ĺ–ł –Ĺ–Ķ—ā–ĺ—á–Ĺ–ĺ—Ā—ā–ł, —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā –≥–ĺ–Ľ—Ź–ľ–ĺ—ā–ĺ –Ĺ–į—Ä–į—Ā—ā–≤–į–Ĺ–Ķ –Ĺ–į –į–ļ—ā–ł–≤–Ĺ–į—ā–į –∑–ĺ–Ĺ–į, –Ĺ–ĺ –Ņ–ĺ–Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ł–∑–Ī–Ķ–≥–Ĺ–į—ā –Ņ–į—ā–ĺ–Ľ–ĺ–≥–ł—á–Ĺ–ł –Ķ—Ą–Ķ–ļ—ā–ł –Ņ–ĺ –ļ—Ä–į–ł—Č–į—ā–į. –Ę–Ķ—Ö–Ĺ–ł–ļ–ł, —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–ĺ –Ņ—Ä–Ķ–ĺ—Ä–į–∑–ľ–Ķ—Ä—Ź–≤–į–Ĺ–Ķ –Ĺ–į –Ņ–ĺ–Ľ–Ķ—ā–ĺ, —Ā—ä—Č–ĺ –ľ–ĺ–≥–į—ā –ī–į –≤–Ľ—Ź–∑–į—ā –≤ —É–Ņ–ĺ—ā—Ä–Ķ–Ī–į, —Ā—ä–∑–ī–į–≤–į–Ļ–ļ–ł –≤—Ā–Ķ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ –ľ–į—Ā–ł–≤, –≤ –ļ–ĺ–Ļ—ā–ĺ –ī–į —Ā–Ķ —Ä–į–∑–≤–ł–≤–į—ā —Ą–ĺ—Ä–ľ–ł—ā–Ķ, –ļ–ĺ–ł—ā–ĺ –ł–∑–Ľ–ł–∑–į—ā –ĺ—ā–≤—ä–ī –Ņ—ä—Ä–≤–ĺ–Ĺ–į—á–į–Ľ–Ĺ–ł—ā–Ķ –≥—Ä–į–Ĺ–ł—Ü–ł.
–ö–į—ā–ĺ –į–Ľ—ā–Ķ—Ä–Ĺ–į—ā–ł–≤–į –Ņ—Ä–ĺ–≥—Ä–į–ľ–ł—Ā—ā–ł—ā–Ķ –ľ–ĺ–≥–į—ā –ī–į –ł–∑–ĺ—Ā—ā–į–≤—Ź—ā –ł–ī–Ķ—Ź—ā–į –ī–į –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā –ī–≤—É–ł–∑–ľ–Ķ—Ä–Ķ–Ĺ –ľ–į—Ā–ł–≤ –ļ–į—ā–ĺ –ł–≥—Ä–į–Ľ–Ĺ–ĺ –Ņ–ĺ–Ľ–Ķ –ł –ī–į —É–Ņ–ĺ—ā—Ä–Ķ–Ī—Ź—ā –ī—Ä—É–≥–į —Ā—ā—Ä—É–ļ—ā—É—Ä–į –ĺ—ā –ī–į–Ĺ–Ĺ–ł, –ļ–į—ā–ĺ –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä –≤–Ķ–ļ—ā–ĺ—Ä –ĺ—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł (X, Y), –≤ –ļ–ĺ–Ļ—ā–ĺ –ī–į —Ā–Ķ –Ņ–į–∑—Ź—ā –∂–ł–≤–ł—ā–Ķ –ļ–Ľ–Ķ—ā–ļ–ł. –Ę–ĺ–∑–ł –Ņ–ĺ–ī—Ö–ĺ–ī –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–≤–į –Ĺ–į —Ą–ĺ—Ä–ľ–į—ā–į –ī–į —Ā–Ķ –ī–≤–ł–∂–ł –Ī–Ķ–∑–Ņ—Ä–Ķ–Ņ—Ź—ā—Ā—ā–≤–Ķ–Ĺ–ĺ –Ņ–ĺ –Ņ–ĺ–Ľ–Ķ—ā–ĺ, —Ā—ā–ł–≥–į –Ņ–ĺ–Ņ—É–Ľ–į—Ü–ł—Ź—ā–į –ī–į –Ĺ–Ķ –Ņ—Ä–Ķ–≤–ł—ą–į–≤–į –≥–ĺ–Ľ–Ķ–ľ–ł–Ĺ–į—ā–į –Ĺ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–į—ā–į —Ā–ł—Ā—ā–Ķ–ľ–į. –Ě–Ķ–ī–ĺ—Ā—ā–į—ā—ä–ļ –Ķ, —á–Ķ –Ņ—Ä–Ķ–Ī—Ä–ĺ—Ź–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –∂–ł–≤–ł—ā–Ķ —Ā—ä—Ā–Ķ–ī–ł —Ā—ā–į–≤–į —á—Ä–Ķ–∑ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ł –∑–į —ā—ä—Ä—Ā–Ķ–Ĺ–Ķ, –ļ–ĺ–Ķ—ā–ĺ –∑–į–Ī–į–≤—Ź —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—ā–į –Ĺ–į —Ā–ł–ľ—É–Ľ–į—Ü–ł—Ź, –Ĺ–ĺ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ–ĺ–ī–ĺ–Ľ–Ķ–Ķ —á—Ä–Ķ–∑ –Ņ—Ä–ł–Ľ–į–≥–į–Ĺ–Ķ –Ĺ–į –Ņ–ĺ-—Ā–Ľ–ĺ–∂–Ĺ–ł —Ā—ā—Ä—É–ļ—ā—É—Ä–ł –ĺ—ā –ī–į–Ĺ–Ĺ–ł.
–ó–į –ī–į —Ā–Ķ —Ā–ł–ľ—É–Ľ–ł—Ä–į –Ķ–≤–ĺ–Ľ—é—Ü–ł—Ź—ā–į –Ĺ–į –≥–ĺ–Ľ—Ź–ľ –Ī—Ä–ĺ–Ļ –ļ–Ľ–Ķ—ā–ļ–ł –≤ –ī—ä–Ľ–≥–ĺ—Ā—Ä–ĺ—á–Ķ–Ĺ –Ņ–Ľ–į–Ĺ, –≤ —É–Ņ–ĺ—ā—Ä–Ķ–Ī–į –≤–Ľ–ł–∑–į—ā –Ņ–ĺ-—Ā–Ľ–ĺ–∂–Ĺ–ł –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ł, –ļ–į—ā–ĺ –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä Hashlife. –°—ä—Č–Ķ—Ā—ā–≤—É–≤–į –ł –ľ–Ķ—ā–ĺ–ī, –Ņ—Ä–ł–Ľ–ĺ–∂–ł–ľ –ł –≤—ä—Ä—Ö—É –ī—Ä—É–≥–ł –ļ–Ľ–Ķ—ā—ä—á–Ĺ–ł –į–≤—ā–ĺ–ľ–į—ā–ł –∑–į –ł–ľ–Ņ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ł–≥—Ä–į—ā–į ‚Äě–Ė–ł–≤–ĺ—ā‚Äú, –Ņ–ĺ–Ľ–∑–≤–į—Č —Ā–Ľ—É—á–į–Ļ–Ĺ–ł –į—Ā–ł–Ĺ—Ö—Ä–ĺ–Ĺ–Ĺ–ł –ĺ–Ī–Ĺ–ĺ–≤—Ź–≤–į–Ĺ–ł—Ź, –ļ–ĺ–ł—ā–ĺ –Ķ–ľ—É–Ľ–ł—Ä–į—ā —ā–ĺ—á–Ĺ–ĺ –Ņ–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ņ—Ä–ł —Ā–ł–Ĺ—Ö—Ä–ĺ–Ĺ–Ĺ–į –ł–ľ–Ņ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ü–ł—Ź.
–°—ä—Č–Ķ—Ā—ā–≤—É–≤–į —Ā–ĺ—Ä—Ā –ļ–ĺ–ī, –Ī–į–∑–ĺ–≤–ĺ –ł–ľ–Ņ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł—Ä–į—Č –ł–≥—Ä–į—ā–į, –Ĺ–į–Ņ–ł—Ā–į–Ĺ –Ĺ–į —Ä–į–∑–Ľ–ł—á–Ĺ–ł –Ķ–∑–ł—Ü–ł –∑–į –Ņ—Ä–ĺ–≥—Ä–į–ľ–ł—Ä–į–Ĺ–Ķ, –≤ —ā.—á. C, C++, Java –ł Python.
–ú–ĺ–ī–ł—Ą–ł–ļ–į—Ü–ł–ł
–°–Ľ–Ķ–ī –ł–≥—Ä–į—ā–į ‚Äě–Ė–ł–≤–ĺ—ā‚Äú —Ā–Ķ —Ä–į–∑–≤–ł–≤–į—ā –Ĺ–ĺ–≤–ł —Ā—Ö–ĺ–ī–Ĺ–ł –ļ–Ľ–Ķ—ā—ä—á–Ĺ–ł –į–≤—ā–ĺ–ľ–į—ā–ł. –°—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–į—ā–į ‚Äě–ė–≥—Ä–į –Ĺ–į –∂–ł–≤–ĺ—ā–į‚Äú —Ā–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ź —Ā—ä—Ā —Ā–ł–ľ–≤–ĺ–Ľ–ł—ā–Ķ ‚ÄěB3/S23‚Äú: –ē–ī–Ĺ–į –ļ–Ľ–Ķ—ā–ļ–į —Ā–Ķ —Ā—á–ł—ā–į –∑–į ‚Äě–†–ĺ–ī–Ķ–Ĺ–į‚Äú (Born), –į–ļ–ĺ –ł–ľ–į —ā–ĺ—á–Ĺ–ĺ 3 —Ā—ä—Ā–Ķ–ī–Ĺ–ł, ‚Äě–ě—Ā—ā–į–≤–į –∂–ł–≤–į‚Äú (Stays Alive), –į–ļ–ĺ –ł–ľ–į 2 –ł–Ľ–ł 3 –∂–ł–≤–ł —Ā—ä—Ā–Ķ–ī–Ĺ–ł –ļ–Ľ–Ķ—ā–ļ–ł, –≤ –Ņ—Ä–ĺ—ā–ł–≤–Ķ–Ĺ —Ā–Ľ—É—á–į–Ļ —É–ľ–ł—Ä–į. –ü—ä—Ä–≤–ĺ—ā–ĺ —É—Ā–Ľ–ĺ–≤–ł–Ķ –ł–Ľ–ł —Ā–Ņ–ł—Ā—ä–ļ –ĺ—ā —É—Ā–Ľ–ĺ–≤–ł—Ź –Ķ —Ā–≤—ä—Ä–∑–į–Ĺ–ĺ —Ā —ā–ĺ–≤–į –ļ–į–ļ–≤–ĺ –Ķ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ, –∑–į –ī–į –ľ–ĺ–∂–Ķ –Ķ–ī–Ĺ–į –ľ—ä—Ä—ā–≤–į –ļ–Ľ–Ķ—ā–ļ–į –ī–į —Ā–Ķ —Ä–ĺ–ī–ł –ĺ—ā–Ĺ–ĺ–≤–ĺ. –°–Ľ–Ķ–ī–≤–į—Č–ł—Ź—ā –Ĺ–į–Ī–ĺ—Ä –≤–ļ–Ľ—é—á–≤–į –ł–∑–ł—Ā–ļ–≤–į–Ĺ–Ķ—ā–ĺ –ļ–į–ļ –Ķ–ī–Ĺ–į –∂–ł–≤–į –ļ–Ľ–Ķ—ā–ļ–į –ī–į –ĺ—Ü–Ķ–Ľ–Ķ–Ķ –ī–ĺ —Ā–Ľ–Ķ–ī–≤–į—Č–ĺ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł–Ķ. –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ ‚ÄěB6/S16‚Äú –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ –Ķ–ī–Ĺ–į –ļ–Ľ–Ķ—ā–ļ–į –Ķ —Ä–ĺ–ī–Ķ–Ĺ–į, –į–ļ–ĺ –ł–ľ–į 6 —Ā—ä—Ā–Ķ–ī–Ĺ–ł, –ł —Č–Ķ –∂–ł–≤–Ķ–Ķ, –ī–ĺ–ļ–į—ā–ĺ –ĺ–ļ–ĺ–Ľ–ĺ –Ĺ–Ķ—Ź –ł–ľ–į 1 –ł–Ľ–ł 6 —Ā—ä—Ā–Ķ–ī–Ĺ–ł. –ö–Ľ–Ķ—ā—ä—á–Ĺ–ł—Ź—ā –į–≤—ā–ĺ–ľ–į—ā –Ĺ–į –ī–≤—É–ľ–Ķ—Ä–Ĺ–į—ā–į —Ä–Ķ—ą–Ķ—ā–ļ–į, –ļ–ĺ–Ļ—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ĺ–Ņ–ł—Ā–į–Ĺ –Ņ–ĺ —ā–ĺ–∑–ł –Ĺ–į—á–ł–Ĺ, –Ķ –Ņ–ĺ–∑–Ĺ–į—ā –ļ–į—ā–ĺ Life-like –ļ–Ľ–Ķ—ā—ä—á–Ķ–Ĺ –į–≤—ā–ĺ–ľ–į—ā. –Ē—Ä—É–≥ —á–Ķ—Ā—ā–ĺ —Ā—Ä–Ķ—Č–į–Ĺ Life-like –į–≤—ā–ĺ–ľ–į—ā ‚Äď Highlife, –Ķ –ĺ–Ņ–ł—Ā–į–Ĺ –ĺ—ā –Ņ—Ä–į–≤–ł–Ľ–ĺ—ā–ĺ ‚ÄěB36/S23‚Äú, –∑–į—Č–ĺ—ā–ĺ –ł–ľ–į–Ļ–ļ–ł 6 —Ā—ä—Ā–Ķ–ī–ļ–ł –ļ–Ľ–Ķ—ā–ļ–ł –≤ –ī–ĺ–Ņ—ä–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ņ—ä—Ä–≤–ĺ–Ĺ–į—á–į–Ľ–Ĺ–ĺ—ā–ĺ –Ņ—Ä–į–≤–ł–Ľ–ĺ –Ĺ–į –ł–≥—Ä–į—ā–į ‚ÄěB3/S23‚Äú, —Ā—ā–į–≤–į –Ņ—Ä–ł—á–ł–Ĺ–į –∑–į —Ä–į–∂–ī–į–Ĺ–Ķ. HighLife –Ķ –ī–ĺ–Ī—Ä–Ķ –Ņ–ĺ–∑–Ĺ–į—ā –∑–į—Ä–į–ī–ł —á–Ķ—Ā—ā–ĺ —Ā—Ä–Ķ—Č–į–Ĺ–ł—ā–Ķ –ľ—É –ī–≤–ĺ–Ļ–Ĺ–ł—Ü–ł. –°—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā –ł –ī–ĺ–Ņ—ä–Ľ–Ĺ–ł—ā–Ķ–Ľ–Ĺ–ł Life-like –ļ–Ľ–Ķ—ā—ä—á–Ĺ–ł –į–≤—ā–ĺ–ľ–į—ā–ł, –≤—ä–Ņ—Ä–Ķ–ļ–ł —á–Ķ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ–į—ā–į —á–į—Ā—ā –ĺ—ā —ā—Ź—Ö —Ā—ä–∑–ī–į–≤–į—ā –≤—Ā–Ķ–Ľ–Ķ–Ĺ–ł, –ļ–ĺ–ł—ā–ĺ –ł–Ľ–ł —Ā–į —ā–≤—ä—Ä–ī–Ķ —Ö–į–ĺ—ā–ł—á–Ĺ–ł, –ł–Ľ–ł —ā–≤—ä—Ä–ī–Ķ –Ņ—É—Ā—ā–ł, –∑–į –ī–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į—ā –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā.
–Ě—Ź–ļ–ĺ–ł –ľ–ĺ–ī–ł—Ą–ł–ļ–į—Ü–ł–ł –Ĺ–į –ł–≥—Ä–į—ā–į –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź—ā –ļ–į–ļ—ā–ĺ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—ā–į –Ĺ–į –≤—Ā–Ķ–Ľ–Ķ–Ĺ–ł—ā–Ķ, —ā–į–ļ–į –ł —Ā–į–ľ–ĺ—ā–ĺ –Ņ—Ä–į–≤–ł–Ľ–ĺ. –ú–ĺ–∂–Ķ–ľ –ī–į –Ņ—Ä–ł–Ķ–ľ–Ķ–ľ, —á–Ķ –≥–ĺ—Ä–Ĺ–ł—ā–Ķ –ľ–ĺ–ī–ł—Ą–ł–ļ–į—ā–ĺ—Ä–ł —Ā–į 2D –ļ–≤–į–ī—Ä–į—ā–ł, –∑–į—Č–ĺ—ā–ĺ —Ā–≤–Ķ—ā—ä—ā –Ķ –ī–≤—É–ł–∑–ľ–Ķ—Ä–Ķ–Ĺ –ł –Ķ –Ņ–ĺ—Ā—ā–į–≤–Ķ–Ĺ –≤ –ļ–≤–į–ī—Ä–į—ā–Ĺ–į —Ä–Ķ—ą–Ķ—ā–ļ–į. 1D –ļ–≤–į–ī—Ä–į—ā–Ĺ–ł—ā–Ķ –ľ–ĺ–ī–ł—Ą–ł–ļ–į—ā–ĺ—Ä–ł (–Ņ–ĺ–∑–Ĺ–į—ā–ł –ļ–į—ā–ĺ –Ņ—ä—Ä–≤–ł—á–Ķ–Ĺ –ļ–Ľ–Ķ—ā—ä—á–Ķ–Ĺ –į–≤—ā–ĺ–ľ–į—ā) –ł 3D –ļ–≤–į–ī—Ä–į—ā–Ĺ–ł—ā–Ķ –ľ–ĺ–ī–ł—Ą–ł–ļ–į—ā–ĺ—Ä–ł —Ā–į –Ī–ł–Ľ–ł —Ä–į–∑—Ä–į–Ī–ĺ—ā–Ķ–Ĺ–ł, —ā—ä–Ļ –ļ–į—ā–ĺ –ł–ľ–į—ā 2D —ą–Ķ—Ā—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł –ł 2D —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł –ľ–ĺ–ī–ł—Ą–ł–ļ–į—ā–ĺ—Ä–ł. –ė–∑—Ä–į–Ī–ĺ—ā–Ķ–Ĺ –Ķ –Ī–ł–Ľ —Ā—ä—Č–ĺ —ā–į–ļ–į –ł –≤–į—Ä–ł–į–Ĺ—ā, –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—Č –Ĺ–Ķ–Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ĺ–į –ľ—Ä–Ķ–∂–į.
–ü—Ä–į–≤–ł–Ľ–ĺ—ā–ĺ –Ĺ–į –ö–ĺ–Ĺ—É–Ķ–Ļ –ľ–ĺ–∂–Ķ —Ā—ä—Č–ĺ –ī–į –Ī—ä–ī–Ķ –ĺ–Ī–ĺ–Ī—Č–Ķ–Ĺ–ĺ —ā–į–ļ–į, —á–Ķ –≤–ľ–Ķ—Ā—ā–ĺ –ī–≤–Ķ —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł—Ź (–∂–ł–≤ –ł–Ľ–ł –ľ—ä—Ä—ā—ä–≤), –ł–ľ–į —ā—Ä–ł –ł–Ľ–ł –Ņ–ĺ–≤–Ķ—á–Ķ. –°–Ľ–Ķ–ī —ā–ĺ–≤–į —Ā—ā–į–ī–ł–Ļ–Ĺ–į—ā–į –Ņ—Ä–ĺ–ľ—Ź–Ĺ–į —Ā–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź –ĺ—ā —Ā–ł—Ā—ā–Ķ–ľ–į –∑–į –Ņ—Ä–Ķ—ā–Ķ–≥–Ľ—Ź–Ĺ–Ķ –ł–Ľ–ł —á—Ä–Ķ–∑ —ā–į–Ī–Ľ–ł—Ü–į, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—Č–į –ĺ—ā–ī–Ķ–Ľ–Ĺ–ł—ā–Ķ –Ņ—Ä–į–≤–ł–Ľ–į –∑–į –Ņ—Ä–Ķ–ľ–ł–Ĺ–į–≤–į –Ĺ–į –≤—Ā—Ź–ļ–ĺ —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä: –≤—Ā—Ź–ļ–ĺ –ĺ—ā –ľ–Ĺ–ĺ–≥–ĺ—Ü–≤–Ķ—ā–Ĺ–į—ā–į ‚Äě–Ę–į–Ī–Ľ–ł—Ü–į —Ā –Ņ—Ä–į–≤–ł–Ľ–į‚Äú –Ĺ–į Mirek's Cellebration –ł —Ą–į–ľ–ł–Ľ–ł—Ź—ā–į –ĺ—ā –Ņ—Ä–į–≤–ł–Ľ–į ‚ÄěWeighted Life‚Äú –≤–ļ–Ľ—é—á–≤–į –Ņ—Ä–į–≤–ł–Ľ–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –Ĺ–į ‚Äě–Ė–ł–≤–ĺ—ā‚Äú.
–í –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł Life-like –ľ–ĺ–ī–ł—Ą–ł–ļ–į—ā–ĺ—Ä–ł –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –Ĺ–į–Ī–Ľ—é–ī–į–≤–į—ā –ł —Ā—ā—Ä—É–ļ—ā—É—Ä–ł, —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā —Ą—Ä–į–ļ—ā–į–Ľ–ł –ł —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ–ł. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä –į–≤—ā–ĺ–ľ–į—ā ‚ÄěB1/S12‚Äú –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į —á–Ķ—ā–ł—Ä–ł –ľ–Ĺ–ĺ–≥–ĺ –Ī–Ľ–ł–∑–ļ–ł –Ņ—Ä–ł–Ī–Ľ–ł–∂–Ķ–Ĺ–ł—Ź –Ĺ–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į –Ĺ–į –°–Ķ—Ä–Ņ–ł–Ĺ—Ā–ļ–ł, –ļ–ĺ–≥–į—ā–ĺ —Ā–Ķ –Ņ—Ä–ł–Ľ–į–≥–į –∑–į –Ķ–ī–Ĺ–į-–Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–į –∂–ł–≤–į –ļ–Ľ–Ķ—ā–ļ–į. –Ę—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ—ä—ā –Ĺ–į –°–Ķ—Ä–Ņ–ł–Ĺ—Ā–ļ–ł —Ā—ä—Č–ĺ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ĺ–į–Ī–Ľ—é–ī–į–≤–į –≤ ‚Äě–ė–≥—Ä–į—ā–į –Ĺ–į –∂–ł–≤–ĺ—ā–į‚Äú –Ĺ–į –ö–ĺ–Ĺ—É–Ķ–Ļ, —á—Ä–Ķ–∑ –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ –Ĺ–į –ī—ä–Ľ–≥–ĺ—Ā—Ä–ĺ—á–Ĺ–ł—Ź —Ä–į—Ā—ā–Ķ–∂ –Ĺ–į –ī—ä–Ľ–≥–į –Ľ–ł–Ĺ–ł—Ź –Ĺ–į –∂–ł–≤–ł –ļ–Ľ–Ķ—ā–ļ–ł —Ā –ī–Ķ–Ī–Ķ–Ľ–ł–Ĺ–į –Ķ–ī–Ĺ–į –ļ–Ľ–Ķ—ā–ļ–į, –ļ–į–ļ—ā–ĺ –ł –≤ Highlife, Seeds (‚ÄěB2/S‚Äú), –ł –Ņ—Ä–į–≤–ł–Ľ–ĺ—ā–ĺ –Ĺ–į –í–ĺ–Ľ—Ą—Ä–į–ľ (Wolfram's Rule 90).
‚Äě–ė–ľ–ł–≥—Ä–į—Ü–ł—Ź‚Äú –Ķ –ľ–ĺ–ī–ł—Ą–ł–ļ–į—ā–ĺ—Ä, –ļ–ĺ–Ļ—ā–ĺ –Ķ –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ–ī–ĺ–Ī–Ķ–Ĺ –Ĺ–į ‚Äě–ė–≥—Ä–į—ā–į –Ĺ–į –∂–ł–≤–ĺ—ā–į‚Äú –Ĺ–į –ö–ĺ–Ĺ—É–Ķ–Ļ, —Ā –ł–∑–ļ–Ľ—é—á–Ķ–Ĺ–ł–Ķ –Ĺ–į —ā–ĺ–≤–į, —á–Ķ –ł–ľ–į –ī–≤–Ķ ‚Äě–∂–ł–≤–ł‚Äú —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł—Ź (—á–Ķ—Ā—ā–ĺ –ł–∑—Ä–į–∑–Ķ–Ĺ–ł –≤ –ī–≤–į —Ä–į–∑–Ľ–ł—á–Ĺ–ł —Ü–≤—Ź—ā–į). –í—Ā–Ķ–ļ–ł –Ņ—ä—ā, –ļ–ĺ–≥–į—ā–ĺ —Ā–Ķ —Ä–ĺ–ī–ł –Ĺ–ĺ–≤–į –ļ–Ľ–Ķ—ā–ļ–į, —ā—Ź –Ņ—Ä–ł–Ķ–ľ–į ‚Äě–∂–ł–≤–ĺ‚Äú —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ, –ļ–ĺ–≥–į—ā–ĺ –Ķ –Ĺ–į–Ļ-–≥–ĺ–Ľ—Ź–ľ–į—ā–į –ĺ—ā —ā—Ä–ł—ā–Ķ –ļ–Ľ–Ķ—ā–ļ–ł, –ļ–ĺ–ł—ā–ĺ —Ā–į —Ā–Ķ —Ä–ĺ–ī–ł–Ľ–ł. –Ę–į–∑–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į, –∑–į –ī–į —Ā–Ķ —Ä–į–∑–≥–Ľ–Ķ–ī–į –≤–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–ł–Ķ—ā–ĺ –ľ–Ķ–∂–ī—É –ļ–ĺ—Ā–ľ–ł—á–Ķ—Ā–ļ–ł –ļ–ĺ—Ä–į–Ī–ł –ł –ī—Ä—É–≥–ł ‚Äě–ĺ–Ī–Ķ–ļ—ā–ł‚Äú –≤ —Ä–į–ľ–ļ–ł—ā–Ķ –Ĺ–į –ł–≥—Ä–į—ā–į. –Ē—Ä—É–≥ –Ņ–ĺ–ī–ĺ–Ī–Ķ–Ĺ –ľ–ĺ–ī–ł—Ą–ł–ļ–į—ā–ĺ—Ä, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ QuadLife, –≤–ļ–Ľ—é—á–≤–į 4 —Ä–į–∑–Ľ–ł—á–Ĺ–ł –∂–ł–≤–ł —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł—Ź. –ö–ĺ–≥–į—ā–ĺ —Ā–Ķ —Ä–ĺ–ī–ł –Ĺ–ĺ–≤–į –ļ–Ľ–Ķ—ā–ļ–į –ĺ—ā 3 —Ä–į–∑–Ľ–ł—á–Ĺ–ł –∂–ł–≤–ł —Ā—ä—Ā–Ķ–ī–Ĺ–ł –ļ–Ľ–Ķ—ā–ļ–ł, —ā—Ź –Ņ—Ä–ł–Ķ–ľ–į —á–Ķ—ā–≤—ä—Ä—ā–į—ā–į —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā. –Ē—Ä—É–≥ —Ā–Ľ—É—á–į–Ļ –ļ–į—ā–ĺ –ł–ľ–ł–≥—Ä–į—Ü–ł—Ź—ā–į, –Ņ—Ä–ł–Ķ–ľ–į –Ņ—Ä–Ķ–ĺ–Ī–Ľ–į–ī–į–≤–į—Č–į—ā–į —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā. –° –ł–∑–ļ–Ľ—é—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –ľ–ĺ–ī–ł—Ą–ł–ļ–į—ā–ĺ—Ä–ł—ā–Ķ —Ā—Ä–Ķ–ī –∂–ł–≤–ł—ā–Ķ –ļ–Ľ–Ķ—ā–ļ–ł, –ī–≤–į –ĺ—ā —ā–Ķ–∑–ł –ľ–ĺ–ī–ł—Ą–ł–ļ–į—ā–ĺ—Ä–ł —Ā–Ķ –ī—ä—Ä–∂–į—ā –Ņ–ĺ —Ā—ä—Č–ł—Ź –Ĺ–į—á–ł–Ĺ –ļ–į—ā–ĺ –∂–ł–≤–ł—ā–Ķ.
–í—ä–Ĺ—ą–Ĺ–ł –Ņ—Ä–Ķ–Ņ—Ä–į—ā–ļ–ł
 –ě–Ī—Č–ĺ–ľ–Ķ–ī–ł—Ź
–ě–Ī—Č–ĺ–ľ–Ķ–ī–ł—Ź