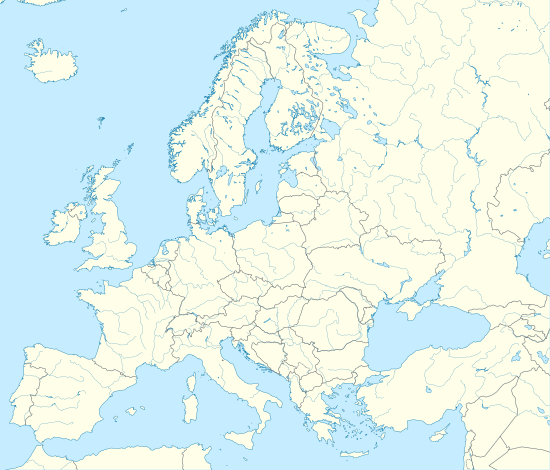
(163364) 2002 OD20 (كويكب)
| ||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

See also: 1951 in art The year 1951 was marked by many events that left an imprint on the history of Soviet and Russian Fine Arts. Events Exhibition Catalog Annual Exhibition of works by Leningrad artists of 1951 was opened in the halls of the Leningrad Union of Artists. The participants were Piotr Alberti, Vladislav Anisovich, Vladimir Avlas, Nikolai Babasuk, Vsevolod Bazhenov, Piotr Belousov, Olga Bogaevskaya, Piotr Buchkin, Rudolf Frentz, Nikolai Galakhov, Vladimir Gorb, Tatiana Kopnina, N...
Ne doit pas être confondu avec Coupe du monde de biathlon 2016-2017. IBU Cup 2016-2017 Généralités Sport Biathlon Organisateur(s) Union internationale de biathlon Éditions 9e Lieu(x) Europe Date 25 novembre 2016 - 12 mars 2017 Épreuves 20 Site web officiel biathlonworld.com Palmarès Vainqueur Alexey Volkov Daria Virolaynen Navigation Édition précédente Édition suivante modifier L'IBU Cup 2016/2017 est la neuvième édition de l'IBU Cup de biathlon. Programme BeitostølenBeitostøle...

Para otros usos de este término, véase Kilmainham (desambiguación). Interior de la prisión de Kilmainham Kilmainham (en Irlandés Cill Mhaighneann) es un suburbio de la ciudad de Dublín, situado al Sur del río Liffey y al Este del centro de la ciudad, en la república de Irlanda. La zona es conocida principalmente por el Real Hospital de Kilmainham, que fue construido donde los Caballeros de San Juan de Jerusalén tuvieron sus priorato. Ahora alberga el Museo Irlandés de Arte Moderno; ...

American sitcom For the ABC talk show of the same name, see The Joey Bishop Show (talk show). The Joey Bishop ShowJoey Bishop and Abby Dalton (1964)GenreSitcomCreated byDanny ThomasLouis F. EdelmanWritten byHarry CraneStan DrebenFred S. FoxFred FreemanIrving ElinsonGarry MarshallDirected byMel FerberJames V. KernJerry ParisStarringJoey BishopAbby Dalton (seasons 2 – 4)Theme music composerVincent Youmans (1961–62)Irving Caesar (1961–62)Jimmy Van Heusen (1962–65)Sammy Cahn (1962–65)Op...

Ishiguro Noboru (石黒昇)Lahir(1938-08-24)24 Agustus 1938 Tokyo, JepangMeninggal20 Maret 2012(2012-03-20) (umur 73) Saiwai, Kawasaki, Prefektur Kanagawa, JapanPekerjaanSutradara, produser, penulis skenario, penyuntingTahun aktif1958 – 2012Suami/istriYumi Ishiguro Noboru Ishiguro (石黒 昇code: ja is deprecated , Ishiguro Noboru, 24 Agustus 1938 – 20 Maret 2012) adalah animator Jepang yang penting untuk mengarahkan serial anime, Space Battleship Yamato, The Supe...

Main airport serving Paris, France Paris Charles de Gaulle AirportAéroport de Paris-Charles-de-GaulleRoissy AirportAéroport de RoissyIATA: CDGICAO: LFPGWMO: 07157SummaryAirport typePublicOwnerGroupe ADPOperatorParis AéroportServesParis metropolitan areaLocationRoissy-en-France, FranceOpened8 March 1974; 49 years ago (1974-03-08)Hub forAir FranceAir France CargoFedEx ExpressOperating base forAir France HopeasyJetElevation AMSL119 m / 392 ftCoordinates49°00�...

2001 single by Gorillaz featuring Del the Funky HomosapienClint EastwoodSingle by Gorillaz featuring Del the Funky Homosapienfrom the album Gorillaz B-sideDraculaReleased5 March 2001 (2001-03-05)StudioStudio 13, London; Geejam, Jamaica; The Glue Factory, San FranciscoGenre Alternative rock[1] alternative hip hop[2] trip hop[3] rap rock[4] dub[4] indie dance[5] Length 5:41 (album version) 5:55 (single version) 3:44 (original mix ed...

Marie Goslich Marie Eva Elwine Goslich (* 24. Februar 1859 in Frankfurt (Oder); † 1938 vermutlich in Obrawalde bei Meseritz) war eine deutsche Fotografin, Schriftstellerin, Erzieherin und Malerin. Inhaltsverzeichnis 1 Leben 2 Fotografische und journalistische Tätigkeit 2.1 Fotografien 2.2 Soziale Themen 2.3 Genrefotografien 2.4 Landschaften 2.5 Zeichnungen 2.6 Journalismus 2.7 Wichtige journalistische Beiträge 3 Ausstellungen 4 Literatur 5 Weblinks Leben Marie Goslich war die Tochter von ...

Village in Sha Tau Kok, Hong Kong Ma Tseuk Leng San Uk Ha (麻雀嶺新屋下) is a walled village. Ma Tseuk Leng San Uk Ha. Former village pond of Ma Tseuk Leng San Uk Ha, with Sha Tau Kok Road in the background. Ma Tseuk Leng (Chinese: 麻雀嶺), sometimes transliterated as Ma Tseuk Ling, is an area in Sha Tau Kok, North District, Hong Kong.[1] The area contains the villages of Ma Tseuk Leng Sheung (麻雀嶺上; 'Upper Ma Tseuk Leng')[2] and Ma Tseuk Leng Ha (�...

Barguna Polytechnic InstituteTypeGovernment Polytechnic InstituteEstablished2006; 17 years ago (2006)Academic staff23[1]Administrative staff27[1]Students1,600[1]LocationBarguna, BangladeshCampusUrban, 2 acres (0.81 ha)[2]AffiliationsBangladesh Technical Education BoardWebsitewww.bargunapoly.gov.bd Barguna Polytechnic Institute This is an image of Barguna polytechnic Institute in Bangladesh.It is the inside view.Barguna Polytechnic Institu...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kynžvart Castle – news · newspapers · books · scholar · JSTOR (March 2013) (Learn how and when to remove this template message) Kynžvart Castle in 2009 Kynžvart Castle (Czech: Zámek Kynžvart; German: Schloss Königswart) is a historic château located near...

Dutch cabinet (1952–1956) Second Drees cabinet Third Drees cabinet45th Cabinet of the Netherlands First meeting of the cabinet in the Trêveszaal on 2 September 1952Date formed2 September 1952 (1952-09-02)Date dissolved13 October 1956 (1956-10-13) 4 years, 41 days in office (Demissionary from 13 June 1956 (1956-06-13))People and organisationsMonarchQueen JulianaPrime MinisterWillem DreesDeputy Prime MinisterLouis BeelNo. of ministers17M...

Bus operator in East of England Go East AngliaParentGo-Ahead GroupFounded2010HeadquartersNorwichService areaEssexSuffolkNorfolkService typeBus & coach servicesDepots5Fleet190[1]Chief executiveGavin SmithWebsiteGo East Anglia Go East Anglia[2] is a bus operator in Essex, Suffolk and Norfolk, owned by the Go-Ahead Group. The group consists of Konectbus and Hedingham & Chambers. History Go East Anglia was initially formed in 2010, when the Go-Ahead Group purchased Konectb...

VEB Robotron Elektronik Dresden. La teoría de la computabilidad o teoría de la recursión es la parte de la computación que estudia los problemas de decisión que se pueden resolver con un algoritmo o equivalentemente con una máquina de Turing. Las preguntas fundamentales de la teoría de la computabilidad son: ¿Qué problemas puede resolver una máquina de Turing? ¿Qué otros formalismos equivalen a las máquinas de Turing? ¿Qué problemas requieren máquinas más poderosas? ¿Qué pr...

Gujarati Poet This article may need to be rewritten to comply with Wikipedia's quality standards. You can help. The talk page may contain suggestions. (March 2015) Dayaram Dayaram (1777–1853) was a Gujarati poet of medieval Gujarati literature and was the last poet of the old Gujarati school. He is known in Gujarati literature for his literary form called Garbi, a lyric song.[1] He was a follower of Pushtimarg of Hindu Vaishnavism.[2] Dayaram, along with Narsinh Mehta and Me...

1998 single by Reba McEntireForever LoveSingle by Reba McEntirefrom the album If You See Him B-sideAll This TimeReleasedJuly 15, 1998GenreCountryLength3:53LabelMCA Nashville 72062Songwriter(s) Liz Hengber Deanna Bryant Sunny Russ Producer(s) David Malloy Reba McEntire Reba McEntire singles chronology If You See Him/If You See Her (1998) Forever Love (1998) Wrong Night (1998) Forever Love is a song recorded by American country music artist Reba McEntire from her studio album, If You See Him (1...

Not to be confused with aiming point. This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (March 2021) (Learn how and when to remove this template message) Aimpoint ABTypePrivate (AB)IndustryManufacturingFounded1974HeadquartersMalmö, SwedenProductsElectro-optical sights and accessoriesWebsitewww.aimpoint.com Aimpoint AB is a Swedish optics company based in Malmö, Sweden tha...

P. Rylands 458 Il Papiro Rylands 458 (P. Rylands 458), datato paleograficamente alla metà del II secolo a.C., è una copia del Pentateuco nella versione greca del Vecchio Testamento conosciuta come Versione dei Settanta o Septuaginta ed è considerata la più antica copia di questa traduzione in greco dell'Antico Testamento. Il manoscritto è stato utilizzato per discutere il Tetragramma, ma contiene solo spazi vuoti in luoghi in cui alcuni studiosi come C. H. Roberts ritengono che dovrebbe ...

Two photographs of a single hologram taken from different viewpoints Holography is a way of making three-dimensional picture with a laser. It allows the holographer to make a more exact image than with photography. The holograph seems to move and change slightly to look as if it were three-dimensional. Holography uses the wave aspect of light. How a hologram is made Holograms are made with light flashed onto a plate or screen, almost like how photos are made. To make a hologram instead of a p...

علي بن حسين الكوتي معلومات شخصية الوفاة سنة 1916 بغداد مكان الدفن مقبرة الغزالي مواطنة الدولة العثمانية الحياة العملية تعلم لدى علي علاء الدين الآلوسي، ومحمود شكري الآلوسي، وعبد الوهاب النائب المهنة فقيه، وعالم مسلم، ومفتي، وكاتب تعديل...




