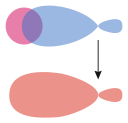
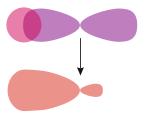
Sigma bond
| ||||||||||||||||
Read other articles:

Merremia aegyptia TaxonomíaReino: PlantaeSubreino: TracheobiontaDivisión: MagnoliophytaClase: MagnoliopsidaSubclase: AsteridaeOrden: SolanalesFamilia: ConvolvulaceaeTribu: MerremieaeGénero: MerremiaEspecie: Merremia aegyptia(L.) Urb.[editar datos en Wikidata] Merremia aegyptia es una especie de planta trepadora perteneciente a la familia Convolvulaceae. Vista de la planta Flor Descripción Son plantas trepadoras perennes; con tallos herbáceos, volubles, generalmente hirsu...

Para otros usos de este término, véase Mimo (desambiguación). El mimo francés Marcel Marceau en 1977. Un mimo (del griego antiguo,[1] ‘mimos’, imitador, actor)[2] es alguien que utiliza la mímica como medio teatral o como una acción artística, o representa una historia a través de gestos faciales o movimientos del cuerpo, sin uso del discurso o expresión verbal.[3][4][a] Orígenes Puede concederse al mimo teatral un origen genérico en el «μ�...

Funiculaire SchlossbergbahnPrésentationType Funiculaire, bien culturelGestionnaire GVB (d)Patrimonialité Objet classé monument historique (en)LocalisationLocalisation Graz AutricheCoordonnées 47° 04′ 30″ N, 15° 26′ 07″ Emodifier - modifier le code - modifier Wikidata Le Schlossbergbahn, ou Schloßbergbahn est un funiculaire de la ville autrichienne de Graz. Il relie le centre-ville à la colline du Schloßberg, avec une vue imprenable sur la vi...

Túpac Amaru III Diputado constituyente de la República del Perúpor Lampa, (Puno) 14 de julio de 1855-2 de noviembre de 1857 Diputado de la República del Perúpor Lampa, (Puno) 16 de abril de 1845-17 de noviembre de 1853 Información personalNacimiento 24 de junio de 1808Vilque, Intendencia de Puno, Virreinato de PerúFallecimiento 3 de enero de 1868 (60 años)Pusi, Puno, PerúNacionalidad peruanaperuanaFamiliaPadres Mariano Bustamante y JiménezAgustina Dueñas y VeraInformación profesio...

Polish linguist and lexicographer Not to be confused with Alexander Brückner. Aleksander BrücknerBorn(1856-01-29)29 January 1856Brzeżany, Galicia, Austrian Empire (now Berezhany, Ukraine)Died24 May 1939(1939-05-24) (aged 83)Berlin, GermanyNationalityPolishOccupation(s)Scholar of Slavic languages and literatures (Slavistics), philologist, lexicographer and historian of literature Aleksander Brückner (Polish pronunciation: [alɛkˈsandɛr ˈbryknɛr]; 29 January 1856 – 2...

1930 film by Thornton Freeland WhoopeeTheatrical release posterDirected byThornton FreelandWritten byWilliam M. ConselmanE.J. Rath (story) Robert Hobart Davis (story)Owen Davis (play)William Anthony McGuire (musical)Produced bySamuel Goldwyn Florenz ZiegfeldStarringEddie CantorEthel ShuttaEleanor HuntCinematographyLee GarmesRay RennahanGregg TolandEdited byStuart HeislerMusic byNacio Herb BrownWalter DonaldsonEdward EliscuColor processTechnicolorProductioncompanySamuel Goldwyn ProductionsDist...

смт Черняхів Герб Черняхова Прапор Черняхова Центральний майдан ЧерняховаЦентральний майдан Черняхова Країна Україна Область Житомирська область Район Житомирський район Громада Черняхівська селищна громада Код КАТОТТГ: Облікова картка смт Черняхів Основн...

العلاقات السويسرية النيجيرية سويسرا نيجيريا سويسرا نيجيريا تعديل مصدري - تعديل العلاقات السويسرية النيجيرية هي العلاقات الثنائية التي تجمع بين سويسرا ونيجيريا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقا�...

Species of shark Milk shark Conservation status Vulnerable (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Chondrichthyes Subclass: Elasmobranchii Subdivision: Selachimorpha Order: Carcharhiniformes Family: Carcharhinidae Genus: Rhizoprionodon Species: R. acutus Binomial name Rhizoprionodon acutus(Rüppell, 1837) Range of the milk shark Synonyms Carcharias aaronis Hemprich & Ehrenberg, 1899 Carcharias acutus Rüppell, 1...

Innuendo Queen Veröffentlichung 14. Januar 1991[1] Länge 6:30 Genre(s) Progressive Rock, Hard Rock Autor(en) QueenFreddie Mercury, Roger Taylor Label Parlophone, Hollywood Album Innuendo Für das Singlecover verwendete Grafik (Grandville, 1844) Innuendo (englisch für „Andeutung“ oder „Anspielung“) ist ein Rocksong der britischen Band Queen. Es wurde am 14. Januar 1991 als Single des gleichnamigen Albums ausgekoppelt und erreichte als dritte Queen-Single nach Bohemian Rhapso...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2015) لينوفو أيديا تاب إيه 3000ملف:Lenovo-ideatab-a3000.jpgمعلومات عامةالنوع حاسوب لوحيالصانع لينوفوعائلة المنتج تاب إيه (بالإنجليزية: TAB A)الجيل الجيل الثالثالتوفر في السو�...

Rujak India Malaysia, atau dikenali sebagai Pasembur. Masakan India Malaysia, atau masakan masyarakat etnis India di Malaysia, terdiri dari adaptasi hidangan otentik dari India, serta kreasi asli yang terinspirasi oleh budaya makanan Malaysia yang beragam. Karena sebagian besar komunitas India Malaysia adalah keturunan India Selatan, dan sebagian besar adalah etnis Tamil yang merupakan keturunan imigran dari wilayah bersejarah yang terdiri dari negara bagian Tamil Nadu di India modern dan Pro...

American television series For the film, see All Is Forgiven (film). All Is ForgivenCreated by Howard Gewirtz Ian Praiser Starring Bess Armstrong Carol Kane Terence Knox Shawnee Smith Valerie Landsburg David Alan Grier ComposerRobert KraftCountry of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes9 (list of episodes)ProductionExecutive producers James Burrows Glen Charles Les Charles Camera setupMulti-cameraRunning time30 minutesProduction companies Charles/Burrows/Ch...

Mountain in the state of Utah Nagunt MesaNagunt Mesa from the westHighest pointElevation7,785 ft (2,373 m)[1]Prominence905 ft (276 m)[1]Parent peakTimber Top Mountain (8,055 ft)[1]Isolation0.90 mi (1.45 km)[2]Coordinates37°26′27″N 113°10′10″W / 37.440949°N 113.169538°W / 37.440949; -113.169538[1]GeographyNagunt MesaLocation in UtahShow map of UtahNagunt MesaNagunt Mesa (the United St...

HeathcoteNew South Wales—Legislative AssemblyInteractive map of district boundaries from the 2023 state electionStateNew South WalesDates current1971–19911999–presentMPMaryanne StuartPartyLaborNamesakeHeathcote, New South WalesElectors56,158 (2019)Area407.04 km2 (157.2 sq mi)DemographicOuter-metropolitan Electorates around Heathcote: Holsworthy Miranda Miranda Campbelltown Heathcote Cronulla Wollondilly Keira Pacific Ocean Heathcote is an electoral district of the Le...

Internet Relay Chat (IRC) client for Microsoft Windows mIRCScreenshot of an unmodified mIRC 7.27 running on Windows 7Original author(s)Khaled Mardam-BeyDeveloper(s)mIRC Co. Ltd.Initial release28 February 1995 (1995-02-28)Stable release7.75[1] / 26 August 2023 Written inC/C++[2]Operating systemWindows XP and laterPlatformIA-32TypeIRC clientLicenseProprietary/TrialwareWebsitewww.mirc.com mIRC (Arabic: إم آي آر سي) is an Internet Relay Chat (IRC) clie...

邯新片母语国家和地区中国語系汉藏语系 漢語族晋語邯新片語言代碼ISO 639-3–Glottolog无晉語邯新片在中國的分布位置(蓝色) 邯新片是晋语的八个片之一,以邯郸话和新乡话为代表。使用于中国大陆山西省与河南省,河北省交界的邯郸市、晋城市、新乡市、焦作市、济源市、安阳市、鹤壁市等地的太行山区,属于晋语与冀鲁官话,中原官话的过渡方言,特点是: 平聲分陰�...

1924 film by D. W. Griffith For the British film, see Isn't Life Wonderful! Isn't Life WonderfulLobby cardDirected byD. W. GriffithWritten byD. W. GriffithBased onIsn’t Life Wonderful?by Geoffrey MossProduced byD. W. GriffithStarringCarol DempsterNeil HamiltonCinematographyHendrik Sartov [fr]Harold S. SintzenichMusic byLouis SilversCesare SoderoProductioncompanyD.W. Griffith ProductionsDistributed byUnited ArtistsRelease date November 23, 1924 (1924-11-23) Runnin...

2009 studio album by The Empire Shall FallAwakenStudio album by The Empire Shall FallReleasedNovember 17, 2009RecordedProvidence, Rhode Island, United StatesGenreMetalcoreLength39:34LabelAngle Side SideProducerMarcus de LisleThe Empire Shall Fall chronology The Empire Shall Fall Demo(2008) Awaken(2009) Singles from Awaken Lords of WarReleased: 2010 Professional ratingsReview scoresSourceRatingSputnikmusic[1] Awaken is the debut studio album by The Empire Shall Fall, released o...

Volcano in New Zealand Aerial view of Maungataketake in 1964 Satellite view of Maungataketake after being quarried (2016) Maungataketake (also Ellett's Mount) is one of the volcanoes in the Auckland volcanic field in New Zealand. It had a 76 m high scoria cone, beside a 100 m wide crater, before they were quarried away. It was the site of a pā. Layers of volcanic tuff and ash from Maungataketake overlay the fallen trunks of the nearby Ihumātao fossil forest. The New Zealand Minist...