Runge's theorem
|
Read other articles:
Il-Birgu Il-Kunsill Lokali tal-BirguCittà VittoriosaDewan lokalIl-BirguBenteng Santo Angelo BenderaLambang kebesaranMotto: Città VittoriosaNegara MaltaPulauMaltaBordersCospicua, Calcara, ŻabbarPemerintahan • Wali kotaJohn Boxall (Partai Buruh)Luas • Total0,5 km2 (0,2 sq mi)Populasi (Maret 2011) • Total2.758 • Kepadatan5,500/km2 (14,000/sq mi)DemonimĠirbi (maskulin), Ġirbija (feminin), Ġirbin (jamak)Zona w...

Mountain in Italy Piz SalientePiz Saliente from southHighest pointElevation3,048 m (10,000 ft)Prominence186 m (610 ft)[1]Parent peakPiz SerraCoordinates46°35′06″N 10°06′06″E / 46.58500°N 10.10167°E / 46.58500; 10.10167GeographyPiz SalienteLocation in the Alps LocationLombardy, Italy (near the Swiss border)Parent rangeLivigno Alps Piz Saliente is a mountain of the Livigno Alps. Its 3,048-metre-high (10,000 ft) summit is ...

הָאֵבוֹלוּצְיָה שֶׁל הָאָדָם היא תהליך ההתפתחות (אבולוציה) של המין האנושי המודרני, אדם נבון (Homo sapiens), כמו גם של מינים נכחדים נוספים בתת-שבט האדם, מתוך קופי אדם קדומים. תהליך זה התרחש במשך כעשרת מיליוני השנים האחרונות, במהלך התקופות הגאולוגיות של המִיוֹקֵן, הפְּלִיוֹקֵן, הפְ�...

Reserve Bank of India(HI) भारतीय रिज़र्व बैंक Area valutaria India ValutaRupia indiana Istituita1º aprile 1935 e 1935 SedeMumbai Sito web Modifica dati su Wikidata · Manuale La Reserve Bank of India (in hindi:भारतीय रिज़र्व बैंक) è la banca centrale dell'Unione indiana, che stabilisce la politica monetaria della rupia indiana. Indice 1 Storia 1.1 Fondazione 1.2 1935–1950 1.3 1950–1960 1.4 1960–1969 1.5 1969...
لمعانٍ أخرى، طالع العامرية (توضيح). قرية العامرية - قرية - تقسيم إداري البلد اليمن المحافظة محافظة حجة المديرية مديرية عبس العزلة عزلة قطبة السكان التعداد السكاني 2004 السكان 287 • الذكور 136 • الإناث 151 • عدد الأسر 41 • عدد المساكن 41 معلومات �...

Peter Hanke (2015) Peter Hanke (* 28. März 1964 in Wien[1][2]) ist ein österreichischer Manager und Politiker (SPÖ). Von 2002 bis Mai 2018 war er Geschäftsführer der Wien Holding. Seit 24. Mai 2018 ist er amtsführender Stadtrat von Landesregierung und Stadtsenat Ludwig I bzw. Ludwig II.[3][4][5] Inhaltsverzeichnis 1 Leben 2 Auszeichnungen (Auswahl) 3 Kontroverse 4 Weblinks 5 Einzelnachweise Leben Peter Hanke ist Sohn des 1933 geborenen sozialdemok...
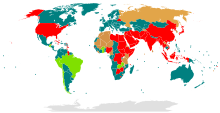
死刑制度の状況を表した世界地図。パプアニューギニアは完全な死刑廃止国であることを示す深緑で塗られている。 本項では、パプアニューギニアにおける死刑(パプアニューギニアにおけるしけい)について解説する。パプアニューギニアでは、オーストラリアの統治下(英語版)にあった1954年を最後に死刑が執行されていない[1]。死刑制度は独立前の1970年に...

Botanical Garden on the Potchefstroom Campus of the North-West University The North-West University Botanical Garden, view towards thatch sculptureThe North-West University Botanical Garden on the Potchefstroom Campus of the North-West University (NWU) is the only botanical garden in the North West Province of South Africa. The Garden spans just under three hectares and is open to the public.[1][2] History The history of the North-West University Botanical Garden dates back to...

MojayanKelurahanKantor Lurah MojayanNegara IndonesiaProvinsiJawa TengahKabupatenKlatenKecamatanKlaten TengahKodepos57416Kode Kemendagri33.10.25.1008 Kode BPS3310720004 Luas1,3 km²Jumlah penduduk4.342 jiwaKepadatan... jiwa/km² Mojayan adalah kelurahan di kecamatan Klaten Tengah, Klaten, Jawa Tengah, Indonesia. Pembagian wilayah Kelurahan Mojayan terdiri dari beberapa kampung : Dukuh Duwet Harapan Mulya Karangduwet Mojayan Ngentak Randusari Sendangan Srago Gede Tegal Mojayan Pendidi...

1976 studio album by Sonny ClarkSonny Clark QuintetsStudio album by Sonny ClarkReleased1976RecordedDecember 8, 1957 & January 5, 1958Van Gelder Studio, Hackensack, New JerseyGenreJazzLength37:47LabelBlue NoteLNJ 70093ProducerAlfred LionSonny Clark chronology Sonny Clark Trio(1957) Sonny Clark Quintets(1976) Cool Struttin'(1958) Professional ratingsReview scoresSourceRatingAllmusic[1] Sonny Clark Quintets is an album by jazz pianist Sonny Clark, recorded for the Blue Note l...

马立峰号一山本名马泽祥出生1909年1月 大清福建省福寧府福安县溪柄乡马厝村(今 中华人民共和国福建省寧德市福安市溪柄镇立峰村)逝世1935年2月8日(1935歲—02—08)(26歲) 中華民國福建省霞浦县上西区凤洋坪(实属 中华苏维埃共和国闽东苏区霞鼎泰县,今 中华人民共和国福建省宁德市柘荣县黄柏乡)国籍 大清 中華民國 中華民國 中华苏维埃共�...

CFS SydneyPart of The Pinetree LineNova Scotia, Canada CFS SydneyCoordinates46°10′03″N 60°09′53″W / 46.16738°N 60.16469°W / 46.16738; -60.16469CodeC-34Site informationControlled by Royal Canadian Air ForceConditionRepurposedSite historyBuilt1952 (1952)Built by Royal Canadian Air ForceIn use1953-1990Garrison informationGarrison211 Radar Squadron[1] Canadian Forces Station Sydney, also known as CFS Sydney, is a former Can...

Class of Australian 2-8-4T locomotives Not to be confused with WAGR K class (1891) or WAGR K class (diesel). WAGR K classK class with a Goldfields Water Supply Scheme pipe train, ca. 1902Type and originPower typeSteamBuilderNeilson & CoSerial number4599-4606, 5040-5045, 5197-5206Total produced24SpecificationsConfiguration: • Whyte2-8-4TGauge3 ft 6 in (1,067 mm)Fuel typeCoalFuel capacity2.75 long tons 0 cwt (6,200 lb or 2.8 t...

For the Balinese dance, see Legong. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Legong film – news · newspapers · books · scholar · JSTOR (Decembe...

E-learning platform This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. See Wikipedia's guide to writing better articles for suggestions. (June 2020) (Learn how and when to remove this template message) MoodleOriginal author(s)Martin DougiamasDeveloper(s)Martin DougiamasMoodle HQMoodle CommunityInitial release20 August 2002; 21 years ago (2002-08-20)Stable release4.3[1] / 9 October 2023; 59 days ago (9 October 2023...

Parque nacional Sierra de las Quijadas SituaciónPaís ArgentinaDivisión Provincia de San LuisSubdivisión Departamentos Belgrano y AyacuchoEcorregión Ecotono entre las ecorregiones del monte de llanuras y mesetas, del monte de sierras y bolsones y chaco árido.Coordenadas 32°33′03″S 67°03′51″O / -32.55083333, -67.06416667Datos generalesAdministración Administración de Parques NacionalesGrado de protección Lista indicativa del Patrimonio de la Hu...

2013 single by HKT48Suki! Suki! Skip!Type A coverSingle by HKT48ReleasedMarch 20, 2013 (2013-03-20) (Japan)GenreJ-popLabelUniversal SigmaSongwriter(s)Yasushi AkimotoProducer(s)Yasushi AkimotoHKT48 singles chronology Suki! Suki! Skip! (2013) Melon Juice (2013) Professional ratingsReview scoresSourceRatingRolling Stone Japan[1] Suki! Suki! Skip! (スキ!スキ!スキップ!, Suki! Suki! Sukippu!) is the first single by Japanese girl group HKT48. It was released in Japan o...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Astro Nusantara – berita · surat kabar · buku · cendekiawan · JSTOR PT Direct VisionNama dagangAstro NusantaraJenisPatunganIndustriTelevisi satelit berlanggananNasibDitutup, dialihkan ke First MediaDidir...

2012 film by V. K. Prakash KarmayogiFilm posterDirected byV. K. PrakashWritten byBalram MattannurBased onHamletby ShakespeareProduced byVachan ShettySajitha PrakashStarringIndrajithNithya MenonPadmini KolhapureSaiju KurupNarrated byRenjithCinematographyR. D. RajasekharEdited byBeena PaulMusic byOusepachanProductioncompaniesTrends Add FilmsInnostorm Entertainment GroupCreative Land PicturesRelease date 16 March 2012 (2012-03-16) CountryIndiaLanguageMalayalam Karmayogi is a 2012 ...

Fictional character from the BBC medical drama Casualty Fictional character Alicia MunroeCasualty characterChelsea Halfpenny as Alicia MunroeFirst appearanceCradle to Grave19 September 2015Last appearanceEpisode 111219 January 2019Portrayed byChelsea HalfpennyIn-universe informationOccupation Specialty registrar, pediatric emergency medicine (prev. Specialty registrar, emergency medicine F2 doctor, emergency medicine) Significant otherEthan HardyCaleb KnightRelativesJackie Munroe (mother)Howa...






