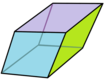
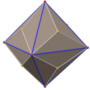
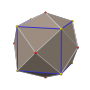
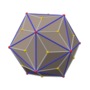
Rhombic triacontahedron
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Pascal Feindouno Feindouno con la maglia della Guinea nel 2006 Nazionalità Guinea Altezza 176 cm Peso 69 kg Calcio Ruolo Attaccante Termine carriera 1⁰ luglio 2016 Carriera Giovanili 1996-1997 Kamsar1998 Hirondelles Squadre di club1 1998-2001 Bordeaux39 (3)2001-2002 Lorient30 (6)2002-2004 Bordeaux102 (21)2004-2008 Saint-Étienne171 (49)2008-2010 Al-Sadd24 (11)2009-2010→ Al-Rayyan14 (5)2010→ Al-Nassr5 (2)2011 Monaco5 (0)2011-2012...

У Вікіпедії є статті про інших людей із прізвищем Осипов.Осипов Альберт НиканоровичДата народження 25 червня 1936(1936-06-25) (87 років)Місце народження Міякинський район, Башкирська АРСР, РСФРР, СРСРГромадянство СРСР УкраїнаAlma mater Всеросійський державний інститут кінемато

Political process behind the American holiday Passage of Martin Luther King Jr. DayLong titleA bill to amend title 5, United States Code, to make the birthday of Martin Luther King, Jr., a legal public holiday.Enacted bythe 98th United States CongressEffectiveJanuary 1, 1986CitationsPublic lawPub. L.Tooltip Public Law (United States) 98–144Statutes at Large97 Stat. 917CodificationU.S.C. sections amended5 U.S.C. § 6103Legislative historyIntroduced in the H...

Quincentennial historical markersThe Suluan Quincentennial markerLocation34 different sites in the PhilippinesDesignerRelief: Jonas Roces and Francis Apiles (based on sketches by muralist Derrick Macutay)TypeHistorical markersDedicated dateMagellan-Elcano expedition in the Philippine archipelago The following is a list of Quincentennial historical markers unveiled by the National Historical Commission and the National Quincentennial Committee as part of the 2021 Quincentennial Commemorat...

Hong Kong actor This article is about the Hong Kong actor. For the American biophysical chemist, see Sunney Chan. For the singer Sunny Chan Si-Sun, see Supper Moment. This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Sunny Chan ...

15th TVyNovelas AwardsDateMay 15, 1997LocationTeatro Alameda, San Ángel, México D.F.Hosted byRaúl Velasco, Marco Antonio Regil, Julissa & Liza EcheverríaMost awardsCañaveral de pasiones (10)Most nominationsLa antorcha encendida (14)Television/radio coverageNetworkCanal de las estrellas ← 14th · TVyNovelas Awards · 16th → The 15th TVyNovelas Awards were an academy of special awards to the best soap operas and TV shows. The awards ceremony took place o...

Comic album by Belgian cartoonist Hergé For other uses, see Black Island. The Black Island (L'Île noire)Cover of the English editionDate 1938 (black and white) 1943 (colour) 1966 (colour remake) SeriesThe Adventures of TintinPublisherCastermanCreative teamCreatorHergéOriginal publicationPublished inLe Petit VingtièmeDate of publication15 April 1937 – 16 June 1938LanguageFrenchTranslationPublisherMethuenDate1966Translator Leslie Lonsdale-Cooper Michael Turner Chr...

لمعانٍ أخرى، طالع بلدة فالي (توضيح). بلدة فالي الإحداثيات 48°19′25″N 95°40′08″W / 48.323611111111°N 95.668888888889°W / 48.323611111111; -95.668888888889 تقسيم إداري البلد الولايات المتحدة التقسيم الأعلى مقاطعة مارتين، مينيسوتا خصائص جغرافية المساحة 33.9 ميل مربع ارتفاع ...

Railway station in Kent, England This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2019) (Learn how and when to remove this template message) East FarleighGeneral informationLocationEast Farleigh, MaidstoneEnglandGrid referenceTQ734536Managed bySoutheasternPlatforms2Other informationStation codeEFLClassificationDfT category F2HistoryOpened25 September 1844...

International network of companies controlled by the Safra family This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Safra Group – news · newspapers · books · scholar · JSTOR (March 2011) (Learn how and when to remove this template message) J. Safra GroupTypePrivateIndustryConglomerateHeadquartersSão Paulo, Br...

El Cubo de Don Sanchocomune El Cubo de Don Sancho – Veduta LocalizzazioneStato Spagna Comunità autonoma Castiglia e León Provincia Salamanca TerritorioCoordinate40°53′30.12″N 6°18′25.92″W / 40.8917°N 6.3072°W40.8917; -6.3072 (El Cubo de Don Sancho)Coordinate: 40°53′30.12″N 6°18′25.92″W / 40.8917°N 6.3072°W40.8917; -6.3072 (El Cubo de Don Sancho) Altitudine736 m s.l.m. Superficie91 km² Abitanti508 (20...

Квантовый газ — газ частиц или квазичастиц, подчиняющийся квантовой статистике. Свойства квантового газа зависят от степени его вырождения, характеризующегося температурой вырождения. Температура вырождения T 0 {\displaystyle T_{0}} зависит от плотности газа, T 0 ∼ N ( 2 / 3 ) m k ...

Pasukan Belanda sedang menyerbu Bone. Pada tahun 1824, serbuan oleh KNIL Belanda ke Kesultanan Bone di Sulawesi Selatan pada tahun 1824 diluncurkan. Latar belakang Setelah jatuhnya Kesultanan Gowa, Kesultanan Bone menjadi yang terkuat di seantero Sulawesi; sejak awal telah merdeka dan menyebarkan pengaruh ke seluruh negeri di Sulawesi; Kesultanan Luwu dan sejumlah negara kecil lain bersekutu dengan Bone, begitupun Kesultanan Soppeng. Setelah peralihan kekuasaan dari Inggris ke Belanda, suasan...

Untuk kegunaan lain, lihat Wadi (disambiguasi). Wadi al'Mujib, Yordania Wadi (Arab: وادي wādī) ialah palung sungai kering yang hanya mengandung air selama hujan lebat. Istilah wādī banyak ditemui dalam toponim bahasa Arab. Wadi cenderung dihubungkan dengan pusat populasi manusia karena tersedianya air bawah tanah. Melintasi wadi yang luas pada waktu-waktu tertentu bisa berbahaya, karena air bah yang tak terduga. Air bah seperti itu menyebabkan kematian tiap tahun di Arab Saudi dan...

Fictional character Olivia (Fringe) redirects here. For the episode with that title, see Olivia (Fringe episode). Fictional character Olivia DunhamFringe characterFirst appearancePilot (episode 1.01)Last appearanceAn Enemy of Fate (episode 5.13)Portrayed byAnna TorvIn-universe informationNicknameLiv, Olive (as a child)OccupationFBI agentFBI interagency liaisonMarine Corps special investigatorFamilyAll Timelines: Marilyn, deceased mother (née unknown)Unnamed father Unnamed uncle (unseen)Unnam...

Czech TV series or program OktopusGenreCrimeCreated byJosef VieweghWritten byJan Pachl, Petr HudskýDirected byJan PachlStarringMiroslav Krobot, Marika Šoposká, Kryštof HádekCountry of originCzech RepublicOriginal languageCzechNo. of seasons1No. of episodes13ProductionCinematographyMarek JandaRunning time60 minutesOriginal releaseNetworkČT1ReleaseAugust 28 (2023-08-28) –November 20, 2023 (2023-11-20) Oktopus is a Czech crime television series. The series is inspired...

GeneralfeldmarschallAlbrecht Graf von RoonAlbrecht von RoonLahir(1803-04-30)30 April 1803Pleushagen, PrusiaMeninggal23 Februari 1879(1879-02-23) (umur 75)Berlin, JermanPengabdian Prusia Kekaisaran JermanDinas/cabangAngkatan Darat PrusiaLama dinas1821–PangkatGeneralfeldmarschallPerang/pertempuranPerang Schleswig Kedua, Perang Austria-Prusia, Perang Prancis-PrusiaPenghargaanPour le Mérite Ordo Elang Hitam Ordo Elang Merah Ordo Wangsa Hohenzollern Ordo Mahkota (Prusia) Or...

この項目では、伝説上の大陸について説明しています。同名の古代ローマの祭り・レムーリア(Lemuria)については「レムレース」を、フィリピンの政治家については「en:Jesus Crispin Remulla」をご覧ください。 レムリア(英語: Lemuria)は、イギリスの動物学者フィリップ・スクレーターが1874年に提唱した、インド洋に存在したとされる仮想の大陸[1][2]。 ま�...

Temidabožica reda i pravednosti.PratiociDika.RoditeljiUran i Geja. Temida (grčki Θέμις, Thémis) je grčka Titanida, božica pravednosti, a u starorimskoj mitologiji je štovana kao Justicija. Temidino ime znači zakon prirode ili red. Po njoj je nazvan asteroid 24 Temis. Opis Temida je personifikacija reda i poretka, zakona i običaja, roditelji su joj Geja i Uran, prvi bogovi. Temida nije osvetoljubiva, već je slatkih obraza. Suci su njezine sluge (themistopoloi). Temida održava re...

Nemzeti Bajnokság I 2007/2008NB I 2006/2007 2008/2009 Szczegóły Państwo Węgry Termin 20 lipca 2007 - 2 czerwca 2008 Liczba meczów 240 Liczba stadionów 16 Zwycięzca MTK Hungária FC Król strzelców Gábor Urbán (11) Sezon 2007/2008 był 105. sezonem Nemzeti Bajnokság I - najwyższej klasy rozgrywkowej na Węgrzech w piłce nożnej. czyli najwyższego poziomu piłkarskiego na Węgrzech. Rozgrywki odbyły się w terminie pomiędzy 20 lipca 2007 a 2 czerwca 2008. Liga liczyła 1...







![{\displaystyle {\begin{aligned}S&=12{\sqrt {5}}\,a^{2}&&\approx 26.8328a^{2}\\[6px]V&=4{\sqrt {5+2{\sqrt {5}}}}\,a^{3}&&\approx 12.3107a^{3}\\[6px]r_{\mathrm {i} }&={\frac {\varphi ^{2}}{\sqrt {1+\varphi ^{2}}}}\,a={\sqrt {1+{\frac {2}{\sqrt {5}}}}}\,a&&\approx 1.37638a\\[6px]r_{\mathrm {m} }&=\left(1+{\frac {1}{\sqrt {5}}}\right)\,a&&\approx 1.44721a\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40d1fe31ccbe520b183e621744df557216cfc9bb)