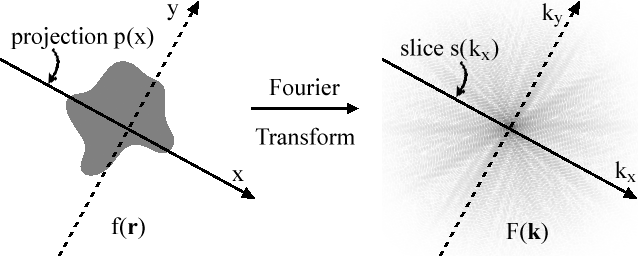
Projection-slice theorem
|
Read other articles:

المسجد الحرام إحداثيات 21°25′21″N 39°49′34″E / 21.4225°N 39.826111111111°E / 21.4225; 39.826111111111 [1] معلومات عامة القرية أو المدينة مكة المكرمة الدولة السعودية الارتفاع عن سطح الأرض 137.5 متر المؤسس النبيان إبراهيم وإسماعيل المجدد انظر أصحاب التوسيعات المواصفات عدد المص�...

Едісон Петтітангл. Edison PettitНародився 22 вересня 1889(1889-09-22)Перу, Немага, Небраска, СШАПомер 6 травня 1962(1962-05-06) (72 роки)Тусон, Аризона, СШАКраїна СШАДіяльність астрономAlma mater Чиказький університетPeru State CollegedГалузь астрономіяЗаклад Обсерваторія Маунт-ВілсонУ шлюбі з Hannah Steele ...

Restaurant Pyongyang in Phnom Penh, Kambodscha Pyongyang ist eine nach der nordkoreanischen Hauptstadt Pjöngjang benannte Restaurantkette mit rund 130 Standorten weltweit.[1] Die Restaurants sind im Besitz der Haedanghwa Group und werden von ihr betrieben. Das Unternehmen ist mutmaßlich eine Tarnfirma der Organisation Office 39, die der Finanzierung des nordkoreanischen Regimes dient.[2] Inhaltsverzeichnis 1 Standorte 2 Angebot 3 Betrieb 4 Weblinks 5 Einzelnachweise Standort...

Karlov Localidad BanderaEscudo KarlovLocalización de Karlov en República ChecaCoordenadas 49°38′49″N 15°54′52″E / 49.647047359979, 15.914476611414Entidad Localidad • País República Checa • Región Vysočina • Distrito Žďár nad SázavouSuperficie • Total 3,04 km² Altitud • Media 636 m s. n. m.Población (1 de enero de 2023) • Total 113 hab. • Densidad 37,22 hab/km²Códi...

CloserAlbum mini karya Oh My GirlDirilis08 Oktober 2015 (2015-10-08)GenreK-popdream popBahasaKoreaLabelWM EntertainmentLOEN EntertainmentProduserLee Won-min72Moon Jeong-gyuKronologi Oh My Girl Oh My Girl(2015)Oh My Girl2015 Closer(2015) Pink Ocean(2016)Pink Ocean2016 Singel dalam album Closer CloserDirilis: 8 Oktober 2015 Closer adalah album mini kedua dari grup vokal wanita asal Korea Selatan Oh My Girl, dirilis pada tanggal 8 Oktober 2015. Lagu yang berjudul Closer digunakan untuk ...

Town in Georgia, United StatesPine Mountain, Georgia ChipleyTownGateway to Callaway GardensLocation in Harris County and the state of GeorgiaCoordinates: 32°51′53″N 84°51′14″W / 32.86472°N 84.85389°W / 32.86472; -84.85389CountryUnited StatesStateGeorgiaCountiesHarris, MeriwetherArea[1] • Total3.18 sq mi (8.24 km2) • Land3.08 sq mi (7.97 km2) • Water0.10 sq mi (0.27 km2)...

Iranian cleric Abdul Fattah NawabSuperintendent of Iranian HujjajIncumbentAssumed office 2019Appointed byAli Khamenei[1][2][3] Personal detailsBorn1957Isfahan, Iran Seyyed Abdul Fattah Nawab (Persian: سید عبدالفتاح نواب) (also: Abdulfattah Nawab)[4][5][6][7] (born: 1957, Shahreza, Isfahan) is an Iranian Twelver Shia cleric who has been recently appointed as the new representative of Guardianship of the Islamic Jurist ...

Public university in Bellingham, Washington Western Washington UniversityFormer namesNorthwest Normal School (1886–1893) MottoMake Waves[1]TypePublic universityEstablishedFebruary 24, 1893; 130 years ago (1893-02-24)Endowment$77.3 million (2019)[2]PresidentSabah RandhawaProvostBrad Johnson[3]Academic staff664 full time(2019)[4]Administrative staff1,437 (2018)[5]Students16,142 (2019)[4]Undergraduates15,240 (2019)[4 ...

Robert F. KennedyKennedy pada tahun 1964Senator Amerika Serikat dari New YorkMasa jabatan3 Januari 1965 – 6 Juni 1968PendahuluKenneth KeatingPenggantiCharles GoodellJaksa Agung Amerika Serikat ke-64Masa jabatan20 Januari 1961 – 3 September 1964PresidenJohn Fitzgerald KennedyLyndon Baines JohnsonPendahuluWilliam P. RogersPenggantiNicholas Katzenbach Informasi pribadiLahirRobert Francis Kennedy(1925-11-20)20 November 1925Brookline, Massachusetts, Amerika SerikatMeninggal6 ...

American singer-songwriter (born 1993) Meghan TrainorTrainor in 2020BornMeghan Elizabeth Trainor (1993-12-22) December 22, 1993 (age 29)Nantucket, Massachusetts, U.S.Occupations Singer-songwriter television personality Years active2009–presentWorks Discography songs Spouse Daryl Sabara (m. 2018)Children2AwardsFull listMusical careerOriginNorth Eastham, Massachusetts, U.S.Genres Pop R&B doo-wop blue-eyed soul Instrument(s) Vocals guitar ukulele ke...

School district in Texas This article needs to be updated. Please help update this article to reflect recent events or newly available information. (March 2022) Crane Independent School DistrictCrane ISD ShieldLocationCrane, TexasESC Region 15 United StatesDistrict informationTypePublicMottoSpreading Far the Fame of the Golden CranesGradesPre-K through 12SuperintendentDr. Stephanie HowardBusiness administratorSylvia VillegasSchool boardVidal Tinker Cadena, Sally Dodd, Rose Mary Cavazos, Azuze...

Operations research that evaluates multiple conflicting criteria in decision making MCDM redirects here. For the use in cosmology, see Meta-cold dark matter. MCDA redirects here. For the technology consortium, see Micro Channel Developers Association. See also: Multi-objective optimization Plot of two criteria when maximizing return and minimizing risk in financial portfolios (Pareto-optimal points in red dots) Multiple-criteria decision-making (MCDM) or multiple-criteria decision analysis (M...

American-born Canadian lawyer and television producer Stephen StohnCMStohn in 2022BornMay 8, 1948 (1948-05-08) (age 75)Denver, Colorado, U.S.Occupation(s)Television producer, entertainment lawyerSpouse Linda Schuyler (m. 1995)ChildrenMax Stohn John Stephen Stohn, CM (born May 8, 1948) is an American-born Canadian entertainment lawyer and television producer. He is best known for his involvement with the Degrassi teen drama franchise, particularly as an...

Ini daftar 100 kota penduduk terbesar di Libya. Beberapa tempat dalam daftar dapat dianggap pinggiran kota atau wilayah di beberapa kota besar di daftar, jadi daftar ini tidak definitif. Tripoli, Ibu kota Libya Benghazi Bayda Misrata Derna Tobruk Brega Sirte Ghadames No. Kota Populasi(2006) 1 Tripoli 1,228,187 2 Benghazi 670,797 3 Misrata 281,000 [1] 4 Bayda 250,000 [2] 5 Zawiya 200,000 [3] 6 Zuwara 180,000 [4] 7 Ajdabiya 108,771 9 Homs 103,743 10 Sabha 94,728 ...

British record producer Not to be confused with Andy Richards (The Young and the Restless). Andy RichardsAndy Richards in his studio, Out of Eden, September 2009Background informationBirth nameAndrew John RichardsBorn (1952-10-26) 26 October 1952 (age 71)London, EnglandGenresPop, rock, folk, jazz, classical, alternative, soundtrackOccupation(s)Musician, composer, producer, film scoring mixer and engineer, music supervisorInstrument(s)Piano, organ, keyboards, synthesizers, Pro Tools music...

Baronía de la Daya Corona de barónPrimer titular Jaime de MasquefaConcesión Felipe II18 de marzo de 1566Actual titular Carlos Doiz de Espejo y de Arróspide[editar datos en Wikidata] Escudo de Daya Nueva y Daya Vieja, de donde fueron Señores, la familia Masquefa. La Baronía de la Daya es un título nobiliario español creado el 18 de marzo de 1566 por el rey Felipe II a favor de Jaime de Masquefa, Noble del Reino de Valencia. El Título fue rehabilitado en 1917 por el rey Alfon...

District in Reykjavík, IcelandGrafarholt and ÚlfarsárdalurDistrictCountryIcelandMunicipalityReykjavíkArea • District22.5 km2 (8.7 sq mi) • Urban3.1 km2 (1.2 sq mi)Population (2012) • District6,176[1]Postal codeIS-113 Úlfarsfell (Icelandic pronunciation: [ˈulvar̥sˌfɛtl̥]) or Grafarholt og Úlfarsárdalur [ˈkraːvarˌhɔl̥t ɔɣ ˈulvar̥sˌaurˌtaːlʏr̥], is a district of Reykjavík, th...

Polish diplomat Karol BachuraPoland Ambassador to AlbaniaIn officeAugust 2016 – January 2021Appointed byAndrzej DudaPresidentBujar NishaniIlir MetaPreceded byMarek JeziorskiSucceeded byMonika Zuchniak-PazdanDeputy High Representative for Bosnia and HerzegovinaIn officeSeptember 2011 – September 2013Appointed byPeace Implementation CouncilPoland Ambassador MacedoniaIn officeDecember 2007 – August 2011Appointed byLech KaczyńskiPresidentBranko CrvenkovskiGjorge ...

Paris Hilton, 2021 Paris Whitney Hilton, (ùr. 17 gromicznika 1981) je amerikańską spiéwôrką ë teatrownicą. Sąd jã ùkôrôł za to, że òna mia narkózënã. To je blós ùzémk artikla. Rôczimë do jegò rozwicégò.

San Agustín Municipio Vista de la localidad de San Agustín. San AgustínLocalización de San Agustín en Bolivia San AgustínLocalización de San Agustín en PotosíCoordenadas 21°09′19″S 67°40′47″O / -21.15527778, -67.67972222Idioma oficial Castellano (español)Entidad Municipio • País Bolivia • Departamento Potosí • Provincia Enrique BaldiviesoHuso horario UTC -4[editar datos en Wikidata] San Agustín es una localidad ...










![{\displaystyle =\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }f(x,y)\,dy\right]\,e^{-2\pi ixk_{x}}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02d83ac57cdc5698f37cff3d7535c27bd32fef52)


