Partition of unity
|
Read other articles:

Júnior Personlig informationFullständigt namnLeovegildo Lins da Gama JúniorFödelsedatum29 juni 1954 (69 år)Födelseort João Pessoa, BrasilienPositionFörsvarare/MittfältareJuniorlag 1973–1974 Flamengo Seniorlag* År1974–19841984–19871987–19891989–1993Totalt Klubb Flamengo Torino Pescara Flamengo SM (GM) 192 0(7)86 (12)62 0(6)70 (10)410 (35) Landslag År1979–1992 Landslag Brasilien SM (GM)74 0(6) Uppdrag som tränare 1993–199419972003 Flamengo Flamengo Corinthian...

Teater Nasional di Yangon Orkestra Simfoni Nasional Myanmar adalah sebuah orkestra nasional Burma (Myanmar). Dibentuk pada tahun 2001, orkestra milik negara yang berbasis di Yangon ini diizinkan untuk mengadakan konser musik klasik di hadapan publik hanya satu kali pada sepuluh tahun pertamanya. Setelah larangan konser dicabut pada Januari 2012, orkestra ini mengadakan pertunjukan publik keduanya pada bulan Juli 2012 dan melakukan debut internasional pada Kuil Angkor Wat di Kamboja, pada Dese...

2013 Indian filmSIMDirected byDiphanWritten byRoyson VellaraProduced byP J ThomasStarringAnn AugustineDeepakManikandanVinod KovoorMusic byGopi Sunder[1]Release date 19 April 2013 (2013-04-19) Running time90 minutesCountryIndiaLanguageMalayalam SIM is a 2013 Malayalam film directed by Diphan, featuring Ann Augustine, Deepak, Manikandan in lead roles. SIM, which is an acronym for Sorry I am Mad,[2] was produced by Royson Vellara.[3] The film was released o...

معهد تسيير التقنيات الحضرية معلومات التأسيس 1981 (منذ 42 سنة) الانتماءات جامعة محمد بوضياف-المسيلة النوع عمومي الموقع الجغرافي المدينة بلدية المسيلة المكان ولاية المسيلة البلد الجزائر الإدارة الرئيس الدكتور ميلي محمد إحصاءات متفرقات الموقع الموقع الرسمي تعديل مصدري - تعد
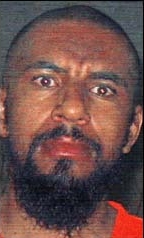
Member of al-Qaeda Abu Yahya al-Libiأبو يحيى الليبيBorn(1973-05-09)9 May 1973Marzaq, LibyaDied4 June 2012(2012-06-04) (aged 39)North Waziristan, PakistanTitleSenior leader of Al-QaedaChildren3 Abu Yahya al-Libi (Arabic: أبو يحيى الليبي, audioⓘ; January 1, 1963,[1] Marzaq[2] – June 4, 2012),[3] born Mohamed Hassan Qaid,[4] was a terrorist and leading high-ranking official within al-Qaeda, and an alleged member of the Libya...

Pour les articles homonymes, voir Banat. Cet article est une ébauche concernant la Serbie et la géographie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Banat méridional Administration Pays Serbie Villesou municipalités PlandišteOpovoKovačicaAlibunarVršacBela CrkvaPančevoKovin Démographie Population 291 327 hab. (2011) Densité 69 hab./km2 Groupes ethniques Serbes, Roumains, Hongrois, S...

Wappen Deutschlandkarte 52.9666666666678.616666666666732Koordinaten: 52° 58′ N, 8° 37′ O Basisdaten Bundesland: Niedersachsen Landkreis: Oldenburg Samtgemeinde: Harpstedt Höhe: 32 m ü. NHN Fläche: 28,18 km2 Einwohner: 978 (31. Dez. 2022)[1] Bevölkerungsdichte: 35 Einwohner je km2 Postleitzahl: 27243 Vorwahl: 04224 Kfz-Kennzeichen: OL Gemeindeschlüssel: 03 4 58 006 Gemeindegliederung: 4 Ortsteile Adresse de...

Hühnchen, Ei und Gemüse in Aspik Aspik ist ein anderer Name für Gelee, das aus Fleisch oder Fisch hergestellt wird. Der Begriff bezeichnet aber auch kalte salzige Gerichte aus unterschiedlichen, meist vorher separat zubereiteten Lebensmitteln, die mit Gelee überzogen sind. Die deutsche Sammelbezeichnung für einige dieser Gerichte ist Sülze. Umgangssprachlich wird Aspik auch „Glibber“[1] genannt. Klassische Rezepte sind z. B. Aal in Gelee, Hummer, Krabben oder Huhn in We...

Petar IRaja Serbia, Kroasia dan SloveniaBerkuasa1 Desember 1918 – 16 Agustus 1921PenerusAleksandar I KarađorđevićWaliPutra Mahkota Aleksandar (1918–1921)Raja SerbiaBerkuasa15 Juni 1903 – 1 Desember 1918Penobatan21 September 1904PendahuluAleksandar I ObrenovićWaliPutra Mahkota Aleksandar (1914–1918)Informasi pribadiKelahiran11 July [K.J.: 29 June] 1844Beograd, Kepangeranan SerbiaKematian16 Agustus 1921(1921-08-16) (umur 77)Beograd, Kerajaan Serbia, Kroasia dan Sloven...

Armed uprising against British Rule in British India Subedar Guddemane Appaiah Gowda in Madikeri The Amara Sullia Rebellion (also called Kalyanappana Katakayi or Amara Sulya Raitha) was an armed uprising against the British government organized by the people of Arebhashe, and Tulunadu that took place in 1837, twenty years before the Sepoy Mutiny of 1857.[1][2][3][4] History In 1799, South Kanara came under British rule. But until Chikkaviraraja (1820–1844), t...

這裡是阿根廷相關旗幟的旗幟列表。 民用旗 (1812年-1985年) 政府旗 軍旗 陸用 民用旗 政府旗 軍用旗 海用 民船旗 政府船旗 軍艦旗 國旗 旗幟 日期 用途 設計 敘述 1818年至今 阿根廷國旗 為天藍、白、天藍三色平行的三色橫旗,中間五月太陽圖樣為國徽。 為阿根廷共和國現今的國旗 1818年至今 阿根廷国旗(垂挂式) 总统旗 旗幟 日期 用途 設計 阿根廷总统旗(西班牙语:Ban...

Not to be confused with EA 2022. EA202 series KfW i9000EA202 series EMU leaving Maguwo StationIn service2013–presentManufacturerIndustri Kereta ApiBombardier TransportationReplacedEA201 seriesConstructed2011Entered service2013Refurbished2019–2020[1]Number built10 sets (40 cars)SuccessorEA203 seriesFormation4 carriages per setFleet numbersK3 1 11 01-K3 1 11 40Capacity628 passengers (average)Operator(s)PT Kereta Commuter IndonesiaLine(s) servedFormer: Jakarta Kota–Bekasi line Duri...

Bandar Udara CharlottetownIATA: YYGICAO: CYYGInformasiJenisSipilPengelolaCharlottetown Airport AuthorityLokasiCharlottetown, Prince Edward IslandZona waktuUTC-4Koordinat{{{coordinates}}} Untuk bandar udara di Newfoundland dan Labrador, lihat Bandar Udara Charlottetown (Newfoundland) Bandar Udara Charlottetown (IATA: YYG, ICAO: CYYG), terletak di Charlottetown, Pulau Pangeran Edward, Kanada. Bandar udara ini dijalankan oleh Charlottetown Airport Authority. Tahun 2004, Bandar udara ini mer...

Sir William MerewetherBorn6 February 1825London, EnglandDied4 October 1880Bayswater, London, EnglandAllegiance United KingdomService/branch British Indian ArmyRankMajor-GeneralBattles/warsAbyssinia ExpeditionAwardsKnight Commander of the Order of the Star of IndiaCompanion of the Order of the Bath Major-General Sir William Lockyer Merewether KCSI CB (6 February 1825 – 4 October 1880) was a Bombay Army officer who served in a number of places including India and Abyssinia.[...

Township in Burlington County, New Jersey, United States Township in New Jersey, United StatesLumberton, New JerseyTownshipCenter of LumbertonLumberton Township highlighted in Burlington County. Inset map: Burlington County highlighted in the State of New Jersey.Census Bureau map of Lumberton, New JerseyLumbertonLocation in Burlington CountyShow map of Burlington County, New JerseyLumbertonLocation in New JerseyShow map of New JerseyLumbertonLocation in the United StatesShow map of the United...

2021 Dutch filmCaptain NovaTheatrical release posterDirected byMaurice TrouwborstWritten byLotte TabbersMaurice TrouwborstProduced byKoji NelissenDerk-Jan WarrinkStarringKika van de VijverAnniek PheiferCinematographyRobbie van BrusselEdited byPelle AsselbergsMusic byAlexander ReumersDistributed byGusto entertainment (Netherlands)Dutch FilmWorks (International)Release date October 13, 2021 (2021-10-13) Running time86 minutesCountryNetherlandsLanguageDutchBox office$129,374[1...

ПамятникПамятник Ази Аслановуазерб. Həzi Aslanovun heykəli 40°21′26″ с. ш. 49°49′46″ в. д.HGЯO Страна Азербайджан Местоположение Баку Скульптор Фуад Абдурахманов Дата основания 1949 Строительство 1949 Медиафайлы на Викискладе Памятник Ази Асланову – надгробный памятник...

Bandar Udara Internasional Tunis-KartagoAéroport international de Tunis-Carthageمطار تونس قرطاج الدوليIATA: TUNICAO: DTTA TUNLokasi bandar udara di TunisiaInformasiJenisPublikPengelolaTunisian Civil Aviation & Airports AuthorityLokasiTunis, TunisiaMaskapai penghubungSyphax Airlines Tunisair TunisAir Express Ketinggian dpl7 mdplKoordinat36°51′04″N 10°13′38″E / 36.85111°N 10.22722°E / 36.85111; 10.22722Situs webwww.tunis-airp...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Alfred VohrerAlfred Vohrer (kedua dari kanan)Lahir(1914-12-29)29 Desember 1914Stuttgart, Kekaisaran JermanMeninggal3 Februari 1986(1986-02-03) (umur 71)Munich, Jerman BaratPekerjaanSutradara, pemeranTahun aktif1958–1984 Alfred Vohrer (29 D...

Castelfidardo Land ItaliaRegion MarcheProvinsProvinsen AnconaStatusKommuneHovedstadCastelfidardo Tilstøtende kommunerCamerano, Loreto, Numana, Osimo, Recanati, Sirolo, Porto RecanatiPostnummer60022Retningsnummer071Areal33,39 km²[1]Befolkning18 419[2] (2023) Bef.tetthet551,63 innb./km²Høyde o.h.215 meter ISTAT-nummer042010Castelfidardo43°27′51″N 13°32′46″ØCastelfidardo på Commons Gatebilde i Castelfidardo. Castelfidardo er en by og kommune i den i...













































![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle f_{1},\ldots ,f_{r}\in \mathbb {C} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68801220a91e7ab98f914a38d20bc3cb54bbd799)





