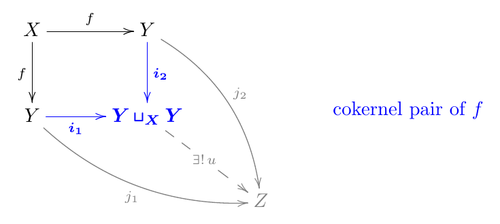
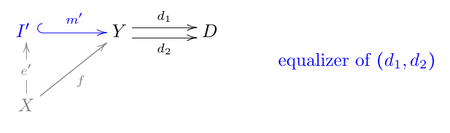
Image (category theory)
|
Read other articles:

マヤ暦(スペイン語: Calendario maya)は、先コロンブス期のメソアメリカ、及びグアテマラの高地[1]やメキシコの一部[2]などの中央アメリカ各地の文明地域(マヤ文明)で使用されていた暦法である。 マヤ暦の本質は、これらの地域で遅くとも紀元前5世紀から一般的に使用されていたシステムに基づいていると考えられている。それは古くはサポテカ文明や

إسماعيل دشتي نائب في مجلس الامة الكويتي معلومات شخصية اسم الولادة إسماعيل علي حاجية دشتي الميلاد 1930 الكويت تاريخ الوفاة 29 نوفمبر 2018 (88 سنة) الجنسية الكويت الديانة مسلم الحياة العملية المهنة سياسي الحزب شيعي - مستقل تعديل مصدري - تعديل إسماعيل علي حاجية دشتي مواليد...

Zetsuen no TempestSampul manga volume pertama yang menampilkan Mahiro Fuwa (kiri) dan Yoshino Takigawa (kanan)絶園のテンペスト(Zetsuen no Tenpesuto)GenreFantasi gelap,[1] misteri[2] MangaPengarangKyō ShirodairaArihide SanoIlustratorRen SaizakiPenerbitSquare EnixImprintGangan ComicsMajalahMonthly Shōnen GanganDemografiShōnenTerbit10 Juli 2009 – 12 Maret 2013Volume10 Seri animeSutradaraMasahiro AndōProduserShunsuke SaitōYasutaka KimuraToshihiro MaedaKōsaku Sakamo...

صدع سيلفرا صدع سيلفرا في المحيط الأطلسي سيلفرا، صدع تم تشكيله في الحدود المتباعدة المتباينة بين أمريكا الشمالية وأوراسيا ويقع في بحيرة بينغفالنتين داخل حديقة ثينغفيلير الوطنية في أيسلندا. التكوين يقع سيلفرا في وادي ثينغفيلير داخل منتزه ثينغفيلير الوطني. تم تشكيل كلا من ال

Species of bird King gull redirects here. For the bird sometimes called king of gulls, see Great black-backed gull. Hartlaub's gull Conservation status Least Concern (IUCN 3.1) Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Charadriiformes Family: Laridae Genus: Chroicocephalus Species: C. hartlaubii Binomial name Chroicocephalus hartlaubii(Bruch, 1855) Synonyms Larus hartlaubii Hartlaub's gull (Chroicocephalus hartlaubii), also...

Map of the United States with Alaska highlighted. Alaska is a state situated in the northwest extremity of the North American continent. According to the 2010 United States Census, Alaska is the 3rd least populous state with 733,391 inhabitants but is the largest by land area spanning 665,384.04 square miles (1,723,336.8 km2) of land.[1][2] As of the 2020 Census, Alaska has 206 census-designated places.[3] Changes for 2020 include the addition of five census-desig...

Ця стаття має кілька недоліків. Будь ласка, допоможіть удосконалити її або обговоріть ці проблеми на сторінці обговорення. Ця стаття потребує упорядкування для відповідності стандартам якості Вікіпедії. Будь ласка, допоможіть поліпшити цю статтю. Можливо, сторінка обгов

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2022) حياة الحقائق La Vie des vérités معلومات الكتاب المؤلف جوستاف لوبون اللغة العربية الناشر دار العالم العربي 2012 مؤسسة هنداوي للتعليم والثقافة 2013 مؤسسة اقرأ للنشر وال�...

Roman golden age (27 BC to 180 AD) For other uses, see Pax Romana (disambiguation). The Pax Romana (Latin for Roman peace) is a roughly 200-year-long timespan of Roman history which is identified as a period and golden age of increased and sustained Roman imperialism, relative peace and order, prosperous stability, hegemonial power, and regional expansion. This is despite several revolts and wars, and continuing competition with Parthia. It is traditionally dated as commencing with the access...

Polish academic Tomasz D. KamusellaKamusella speaking at the First Codification Conference of the Silesian Language in June 2008BornTomasz Dominik Kamuzela (1967-12-24) 24 December 1967 (age 55)Kędzierzyn, Opole Voivodeship, PolandAcademic backgroundAlma materUniversity of Silesia in KatowiceAcademic workSub-disciplineLanguage Politics, Nationalism Studies, History of Central and Eastern EuropeInstitutionsUniversity of St Andrews Tomasz Kamusella FRHistS (born 24 December 1967) is a Pol...

College football game2007 San Diego County Credit Union Poinsettia Bowl Utah Utes Navy Midshipmen (8–4) (8–4) 35 32 Head coach: Kyle Whittingham Head coach: Ken Niumatalolo 1234 Total Utah 071414 35 Navy 010715 32 DateDecember 20, 2007Season2007StadiumQualcomm StadiumLocationSan Diego, CaliforniaMVPBrian Johnson (Utah)FavoriteUtah by 9[1]RefereeTom McCabe (MAC)Halftime showUnited States Naval Academy BandPride of Utah Marching BandAttendance39,129PayoutUS$750,0...

Portaal Bier Brouwerij 'De Ploeg' in Wieze, waar Octaaf Callebaut later de chocolaterie Callebaut vestigde De Brouwerij Callebaut is een voormalige brouwerij in het Belgische dorp Wieze. De brouwerij was actief van 1850 tot 1976. Als chocoladeproducent bestaat het bedrijf nog steeds onder de naam Barry Callebaut. Geschiedenis In 1850 werd de brouwerij opgericht door Eugenius Callebaut. Vanaf 1911 werden er ook chocoladerepen geproduceerd. De schoonzoon van de brouwersfamilie, Arthur Van Den B...

Not to be confused with Stjepan Božić. This article's lead section may not adequately summarize its contents. Please help improve the lead by writing an accessible overview. (July 2012) Stipe BožićBorn(1951-01-02)2 January 1951Zavojane near Vrgorac,PR Croatia, FPR Yugoslavia(today's Croatia)NationalityCroatianOccupation(s)Mountaineer, documentary filmmaker, photographer and writerKnown forCompleted the Seven Summits Stipe Božić (born 2 January 1951[1]) is a Croatian mountai...

Species of moth Swammerdamia caesiella Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Lepidoptera Family: Yponomeutidae Genus: Swammerdamia Species: S. caesiella Binomial name Swammerdamia caesiella(Hübner, 1796)[1] Synonyms Tinea caesiella Hübner, 1796 Swammerdamia heroldella Hübner, [1825] Swammerdamia heroldella Tinea nubeculella Tengström, 1848 Swammerdamia nubeculella Tinea griseocapitella Stainton, 1851 Swammerdami...

Muhammad IIISultan GranadaBerkuasaApril 1302 – 14 Maret 1309PendahuluMuhammad II al-FaqihPenerusNasrInformasi pribadiWangsaBanu NashriAyahMuhammad II al-FaqihAgamaIslamMuhammad III (1257 - setelah 1309) adalah putra dari Muhammad II al-Faqih dan penguasa Banu Nashri ketiga dari Keamiran Granada di Al-Andalus di Semenanjung Iberia. Pada 8 April, 1302 ia naik takhta menjadi Sultan Granada setelah kematian ayahnya Muhammad II al-Faqih. Selama beberapa minggu pertama masa pemerintahannya, Muham...

Hollywood DreamsAlbum studio karya Cinta LauraDirilis16 Juli 2012 (Jakarta, Indonesia)DirekamJuni 2011-Januari 2012(Jakarta, Indonesia; Los Angeles, Amerika)GenrePop, dance-pop, electropopDurasi40:04BahasaIndonesia, InggrisLabelSony Music IndonesiaMusic Factory IndonesiaProduserJan Djuhana, Toto Widjojo; DJ Sumantri; Joachim Svare; Steve Smith, Anthony Anderson; Herdiana KiehlKronologi Cinta Laura Cinta Laura(2010)Cinta LauraString Module Error: Match not found Hollywood Dreams(2012) Sing...

La zarevna rana (o La princesa rana), de Viktor Vasnetsov, habla de una rana que se metamorfosea en una princesa. Louhi, señora del Norte, atacando a Väinämöinen en forma de águila gigante con sus tropas a la espalda cuando intentaba robar el sampo; en el poema épico finlandés Kalevala de Elias Lönnrot. (La defensa del Sampo, Akseli Gallen-Kallela, 1896) El gigante Galligantua y el malvado mago anciano transforman a la hija del duque en una cierva blanca, por Arthur Rackham Loge finge...

2013 American filmCrushTheatrical released posterDirected byMalik BaderWritten bySonny MallhiProduced by Trevor Macy Marc D. Evans Sonny Mallhi Starring Lucas Till Crystal Reed Sarah Bolger Caitríona Balfe Reid Ewing Leigh Whannell CinematographyScott KevanEdited byJeff W. CanavanMusic byJulian BoydProductioncompanyIntrepid PicturesDistributed byFilmNation EntertainmentRelease date April 9, 2013 (2013-04-09) Running time94 minutes[1]CountryUnited StatesLanguageEnglishB...

High school in Union County, New Jersey, United States Mother Seton Regional High SchoolMother Seton Regional High SchoolAddress1 Valley RoadClark, (Union County), New Jersey 07066United StatesCoordinates40°37′32″N 74°18′12″W / 40.62556°N 74.30333°W / 40.62556; -74.30333InformationTypePrivate, All-GirlsReligious affiliation(s)Roman Catholic,Sisters of CharityPatron saint(s)St. Elizabeth Ann SetonEstablished1963NCES School ID00861321[3]PrincipalSr. J...

Public transportation in Taiyuan, Shanxi, China Not to be confused with Taoyuan Metro. Taiyuan MetroOverviewLocaleTaiyuan, Shanxi, ChinaTransit typeRapid transitNumber of lines1Number of stations23Websitewww.tymetro.ltdOperationBegan operation26 December 2020; 2 years ago (2020-12-26)TechnicalSystem length23.65 km (14.70 mi)[1] System map The Taiyuan Metro is a rapid transit system in Taiyuan, capital of China's Shanxi province. The system opened on Decembe...