Earl Young (drummer)
| |||||||||||||||||||
Read other articles:

В Википедии есть статьи о других людях с фамилией Хрущёв. Константин Дмитриевич Хрущёвнем. Konstantin von Chrustschoff Дата рождения 1852[1] Место рождения Веймар, Германский союз[2] Дата смерти 19 апреля 1912(1912-04-19) или 1912[1] Место смерти Санкт-Петербург, Российская импери

Artikel ini bukan mengenai Partai Golongan Karya atau Partai Berkarya. Partai Karya Perjuangan Ketua umumJackson A. KumaatSekretaris JenderalAmbo EnreDibentuk2007Kantor pusatDKI JakartaIdeologiPancasilaKursi di DPRTidak adaSitus webhttp://www.partaikaryaperjuangan.orgPolitik IndonesiaPartai politikPemilihan umum Partai Karya Perjuangan adalah salah satu partai politik di Indonesia. Dalam Pemilu 2009, partai ini bernomor urut 17. Direncanakan pada tahun 2014, Partai ini akan berubah nama ...

لمعانٍ أخرى، طالع نيو هوب (توضيح). نيو هوب الإحداثيات 33°12′45″N 96°33′54″W / 33.2125°N 96.565°W / 33.2125; -96.565 تقسيم إداري البلد الولايات المتحدة[1] التقسيم الأعلى مقاطعة كولين، تكساس خصائص جغرافية المساحة 3.730851 كيلومتر مربع3.730848 كيلومتر مربع (1 أبر

Godfather Godfather (coquetel)Um Godfather servido num copo Old Fashioned Tipo Coquetel Sabor Uísque O Godfather é uma bebida alcoólica, ou um coquetel feito com as bebidas uísque escocês e amaretto.[1] Tipicamente, a bebida é servida com gelo em um copo de vidro do tipo old fashioned. O coquetel é classificado pela International Bartenders Association (IBA) como um clássico e contemporâneo e ideal para consumo após uma refeição.[2] História O Godfather é um coquetel relativamen...

لمعانٍ أخرى، طالع جون أونيل (توضيح). جون أونيل معلومات شخصية الميلاد 3 يناير 1974 (العمر 49 سنة)غلاسكو مركز اللعب وسط الجنسية المملكة المتحدة المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1991–1994 نادي كوينز بارك 91 (30) 1994–1996 سلتيك 2 (0) 1996–2000 بورنموث 125 (10) 2000–2001 روس كاونتي 2 ...

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Março de 2014) Adelaide Princesa de Löwenstein-Wertheim-Rosenberg Adelaide de Löwenstein-Wertheim-RosenbergPrincesa Adelaide, em 1885 Nascimento 3 de abril de 1831 Kleinheubach, Alemanha Morte 16 de dezembro de 1909 (78 ...

2008 Baltimore OriolesLeagueAmerican LeagueDivisionEastBallparkOriole Park at Camden YardsCityBaltimoreRecord68–93 (.421)Divisional place5thOwnersPeter AngelosGeneral managersAndy MacPhailManagersDave TrembleyTelevisionMASNWJZ-TV (CBS 13)RadioWHFS ← 2007 Seasons 2009 → The Baltimore Orioles entered the 2008 season led by Dave Trembley, now starting his first full season as manager. President of Baseball Operations Andy MacPhail continued the rebuilding process. Su...

SassuoloNama lengkapUnione Sportiva Sassuolo Calcio SrlJulukanI Neroverdi (Hitam dan Hijau)Berdiri1922; 100 tahun lalu (1922)StadionStadion Mapei – Città del Tricolore, Reggio Emilia(Kapasitas: 23.717[1])PemilikMapeiPresiden Carlo RossiPelatih Alessio DionisiLigaSerie A2022–2023Serie A, ke–13 dari 20Situs webSitus web resmi klub Kostum kandang Kostum tandang Kostum ketiga Musim ini Unione Sportiva Sassuolo Calcio adalah sebuah klub sepak bola Italia yang berada d...

معهد تاريخ الفن في فلورنسامعلومات عامةالبداية 1897[1] الاسم الرسمي Kunsthistorisches Institut in Florenz (بالألمانية) (1897 – ) مجال العمل دراسة تاريخ الفن المدير Gerhard Wolf (en) البلد إيطاليا[2] تقع في التقسيم الإداري فلورنسا[2] الإحداثيات 43°47′N 11°16′E / 43.78°N 11.26°E / 43.78; 11.26 المن�...

Kabupaten Kulon Progo KulonprogoKabupatenTranskripsi bahasa daerah • Hanacarakaꦏꦸꦭꦺꦴꦤ꧀ꦥꦿꦒSearah jarum jam dari atas : Waduk Sermo, Puncak Moyeng Girimulyo, Patung Nyi Ageng Serang di Wates LambangJulukan: Kota West ProgKota MenorehMotto: ꦲꦩꦩꦪꦸꦲꦪꦸꦤꦶꦁꦧꦮꦤHamemayu hayuning bawana(Jawa) Memperindah keindahan dunia[[File:{{{peta}}}|250px|Peta]]PetaKabupaten Kulon ProgoPetaTampilkan peta IndonesiaKabupaten Kulon ProgoKab...

Railway station in Ōita, Ōita Prefecture, Japan Ōita-Daigaku-mae Station大分大学前駅Ōita-Daigaku-mae Station in 2006General informationLocationJapanCoordinates33°10′38″N 131°37′08″E / 33.17722°N 131.61889°E / 33.17722; 131.61889Operated by JR KyushuLine(s)■ Hōhi Main LineDistance138.8 km from KumamotoPlatforms1 side platformTracks1ConstructionStructure typeAt gradeBicycle facilitiesDesignated parking area for bikesAccessibleYes - ramp to platfo...

Untuk kegunaan lain, lihat Demi Cinta. Demi CintaSutradara Matnoor Tindaon Produser Merry Gultom Soegiman Djajaprawira Ditulis oleh Narto Erawan PemeranSophan SophiaanWidyawatiAedy MowardDina MarianaFadlyMansjur SjahMieke WijayaUci IndrajayaDistributorPanorama FilmTanggal rilis1974Durasi96 menitNegara Indonesia Bahasa Indonesia Demi Cinta adalah film Indonesia yang dirilis pada tahun 1974 dengan disutradarai oleh Matnoor Tindaon. Film ini dibintangi antara lain oleh Sophan Sophiaan dan Widyaw...

For other people with similar names, see Isaac Pardo and Isaac Díaz Pardo. Isaac José PardoBorn(1905-10-14)14 October 1905Caracas, VenezuelaDied3 March 2000(2000-03-03) (aged 94)Caracas, VenezuelaOccupationHistorian, physicianNationalityVenezuelan GenreHistory, essaySubjectHistory of VenezuelaNotable awardsNational Prize for Literature of Venezuela 1984 Signature Isaac José Pardo Soublette (Caracas, 14 October 1905 - 3 March 2000), was a Venezuelan intellectual of German-Jewish extrac...
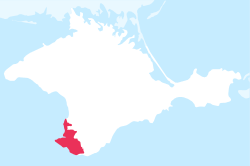
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sevastopol Police – news · newspapers · books · scholar · JSTOR (August 2016) (Learn how and when to remove this template message) Управление МВД России по городу СевастополюMVD's Directorate of Sevastopol CityCommon n...

1st-millennium BCE Canaanite shrine Bamot במות (singular במה bamah) or high places are simple hilltop installations with instruments of religion: platforms, altars, standing stones, and cairns are common. Along with open courtyard shrines and sacred trees or groves, they were of the most often-seen public places of piety in the ancient near East. They appear in the early Bronze Age at latest.[1] Hebrew Bible The bamah of Megiddo From the Hebrew Bible and from existing remains a...

В Википедии есть статьи о других людях с такой фамилией, см. Сидорин.Александр Иванович Сидорин Дата рождения 2 марта 1924(1924-03-02) Место рождения Кладбищи, Алатырский уезд, Симбирская губерния, СССР Дата смерти декабрь 1943 (19 лет) Место смерти Коростенский район[d], Жито...

Yau Kung Moon LogoYau Kung Mun (also Yau Kung Moon) 柔功門 is a Shaolin martial art. The Chinese term, 柔功門, can be roughly translated as the style of flexible power. The Hong Kong and US schools usually use the romanization Yau Kung Moon or Yau Kung Mon, whereas the Australian schools use the romanization Yau Kung Mun. Origins This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and remo...

Single-barrel autocannon M39 M39 cannon in the nose of a Brazilian F-5TypeSingle-barrel autocannonPlace of originUnited StatesService historyIn service1952–presentProduction historyDesignerFord Motor CompanyDesigned1951ManufacturerPontiac, Ford, FMC Corporation, and othersNo. built35,500+VariantsM39, M39A1, M39A2, M39A3SpecificationsMass80.9 kg (178.5 lb)Length1.83 mCartridge20×102mmCaliber20 mm (0.8 in)BarrelsSingle barrel (progressive RH parabolic twist, 9 g...

Artikel ini tentang tahun 1953. 1953MileniumMilenium ke-2AbadAbad ke-19Abad ke-20 Abad ke-21Dasawarsa 1930-an1940-an1950-an1960-an1970-anTahun1950195119521953195419551956 1953 (MCMLIII) merupakan tahun biasa yang diawali hari Kamis dalam kalender Gregorian, tahun ke-1953 dalam sebutan Masehi (CE) dan Anno Domini (AD), tahun ke-953 pada Milenium ke-2, tahun ke-53 pada Abad ke-20, dan tahun ke- 4 pada dekade 1950-an. Denominasi 1953 untuk tahun ini telah digunakan sejak periode Abad Perten...

El algoritmo de Greiner-Hormann es utilizado en computación gráfica para recortar polígonos.[1] Es más eficiente que el algoritmo de Vatti, pero no puede gestionar eventuales casos degenerados.[2] Puede sin embargo utilizarse con polígonos que se auto-intersectan sin ser convexos. Puede fácilmente ser generalizado con el fin de efectuar otras operaciones booleanas sobre polígonos, tales que la unión y la diferencia. Ejemplo de polígonos que se intersectan. El algoritmo ...

