Digital geometry
|
Read other articles:

Карта Азербайджану Державний кордон Азербайджану (азерб. Azərbaycan Respublikasının Dövlət Sərhədi) — державний кордон, лінія на поверхні Землі та вертикальна поверхня, що проходить по цій лінії, що визначають межі державного суверенітету Азербайджану над власними територією, вода�...

ChūkyōKaisar JepangBerkuasa1221PendahuluJuntokuPenerusGo-HorikawaKelahiran30 Oktober 1218Kematian18 Juni 1234 (usia 16)PemakamanKujō no Misasagi (Kyoto) Kaisar Chūkyō (仲恭天皇code: ja is deprecated , Chūkyō-tennō) (30 Oktober 1218 – 18 Juni 1234) adalah kaisar Jepang ke-85. Genealogi Dia adalah putra pertama dari Kaisar Juntoku. Ibunya adalah Ritsuko (?) (立子), putri dari Kujō Yoshitsune (九条良経). Lihat pula Kaisar Jepang Referensi Brown, Delmer M. and Ichirō Ishida,...

Brazilian footballer In this Portuguese name, the first or maternal family name is Gonçalves and the second or paternal family name is Almeida. Stéfano Yuri Stéfano Yuri in 2016Personal informationFull name Stéfano Yuri Gonçalves AlmeidaDate of birth (1994-04-27) 27 April 1994 (age 29)Place of birth Vazante, BrazilHeight 1.87 m (6 ft 1+1⁄2 in)Position(s) StrikerTeam informationCurrent team GoiâniaYouth career2009–2012 Uberlândia2012–2014 SantosSenior c...

Der Titel dieses Artikels ist mehrdeutig. Zum britischen Rechtsrock-Musiker, der diesen Namen als Pseudonym benutzte, siehe Paul Burnley. Paul London Vereinigte Staaten Personalia Geburtsname Paul Michael London Geburtstag 16. April 1980 Geburtsort Austin, Texas, USA Karriereinformationen Ringname(n) Paul LondonEl Gran Luchadore El Vegas Dragon Körpergröße 178 cm Kampfgewicht 93 kg Angekündigt aus Austin, Texas Trainiert von Dory Funk, Jr.Ivan PutskiRudy Boy GonzalesShawn Michaels Debüt ...

1983 American filmThe PassingVHS coverDirected byJohn HuckertWritten byJohn HuckertMary MarucaProduced byJohn HuckertMary MarucaStarringJames Carroll PlasterWelton Benjamin JohnsonJohn HuckertEdited byJohn HuckertRelease date1983Running time96 minutes[1][2]CountryUnited StatesLanguageEnglish The Passing is a 1983 American science fiction horror film co-written, co-produced, directed, edited by and starring John Huckert. Cast James Carroll Plaster as Ernie Neuman Welton Benjami...

She's Out of My LeagueOfficial posterSutradara Jim Field Smith ProduserJimmy MillerDavid HouseholterDitulis olehSean AndersJohn MorrisPemeranJay BaruchelAlice EveMike VogelT.J. MillerNate TorrenceKrysten RitterGeoff StultsLindsay SloanePenata musikMichael AndrewsSinematograferJim DeanultPenyuntingDan SchalkPerusahaanproduksiDreamWorks PicturesMosaic Media GroupDistributorParamount PicturesTanggal rilis 12 Maret 2010 (2010-03-12) Durasi104 menitNegara Amerika Serikat Bahasa Inggris ...

Fictional character on Shortland Street Soap opera character Emily DevineShortland Street characterPortrayed byMichaela RooneyDuration1995–1997, 2019–2020First appearanceDecember 1995Last appearance7 July 2020ClassificationFormer; regularIntroduced byGavin Strawhan (1995)Maxine Fleming (2019)In-universe informationOccupationPathologist Emily Devine is a fictional character on the New Zealand soap opera Shortland Street portrayed by Michaela Rooney. Appearing for two ye...

1995 American filmHideawayTheatrical release posterDirected byBrett LeonardScreenplay byAndrew Kevin WalkerNeal JimenezBased onHideawayby Dean KoontzProduced byJerry A. BaerwitzGimel EverettAgatha HanczakowskiStarring Alicia Silverstone Jeff Goldblum Christine Lahti Alfred Molina Jeremy Sisto CinematographyGale TattersallEdited byB.J. SearsMusic byTrevor JonesProductioncompanyTriStar PicturesDistributed bySony Pictures ReleasingRelease date March 3, 1995 (1995-03-03) Running ti...

IndonesiaFIBA zoneFIBA AsiaWorld CupAppearancesNoneAsian ChampionshipAppearances5 (1980, 1990, 1992, 2008, 2016)MedalsNone The Indonesia women's national under-18 basketball team is a national basketball team of Indonesia, administered by the Indonesian Basketball Association PERBASI.[1] It represents the country in international under-18 (under age 18) women's basketball competitions. Competitions FIBA Women's Asia Cup Asian Cup Record Year Division A Division B Position Pld W L Posi...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) أرسلان محمد باشا معلومات شخصية مكان الميلاد جبلة تاريخ الوفاة سنة 1704 مواطنة الدولة العثمانية م...

Scottish born Irish-American political journalist and writer For other people named Alexander Cockburn, see Alexander Cockburn (disambiguation). This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Alexander Cockburn – news · newspapers · books · scholar · JSTOR (August 2017) (Learn how and when to remove this template message) Alexander CockburnCockburn in ...

National Rail station in London, England Not to be confused with St. John's railway station on the Isle of Man. St Johns St JohnsLocation of St Johns in Greater LondonLocationSt JohnsLocal authorityLondon Borough of LewishamManaged bySoutheasternStation codeSAJDfT categoryENumber of platforms2Fare zone2National Rail annual entry and exit2017–18 0.682 million[1]2018–19 1.001 million[1]2019–20 1.039 million[1]2020–21 0.267 million[1]2021–22 0.646 millio...

Pito de Elliot Estado de conservaciónPreocupación menor (UICN 3.1)[1]TaxonomíaReino: AnimaliaFilo: ChordataClase: AvesOrden: PiciformesFamilia: PicidaeGénero: MesopicosEspecie: M. elliotii(Cassin, 1863)Sinonimia Dendropicos elliotii[2] [editar datos en Wikidata] El pito de Elliot (Mesopicos elliotii)[3] es una especie de ave piciforme de la familia Picidae, que vive en África Central. Distribución y hábitat Se encuentra en los bosques de galer...

Road in Mumbai Jogeshwari–Vikhroli Link Road (JVLR)The JVLR (in purple) linking the Western and Eastern Express Highways (in green).Route informationMaintained by Brihanmumbai Municipal CorporationLength10.6 km (6.6 mi)Existed1994–presentMajor junctionsWest endWestern Express Highway, JogeshwariMajor intersectionsSaki Vihar Road in ChandivaliLBS Marg in Gandhi Nagar, VikhroliEast endEastern Express Highway,Vikhroli LocationCountryIndiaStatesMaharashtraDistrictsMum...

District of Malaysia in KelantanKota Bharu District District of MalaysiaJajahan Kota BharuOther transcription(s) • Jawiكوت بهارو • Chinese哥打峇鲁县 • Tamilகோத்தா பாரு FlagLocation of Kota Bharu District in KelantanKota Bharu DistrictLocation of Kota Bharu District in MalaysiaCoordinates: 6°5′N 102°16′E / 6.083°N 102.267°E / 6.083; 102.267Country MalaysiaState KelantanSea...

Snow patrol redirects here. For the rescue service for skiers and participants in other snow sports, see Ski patrol and Mountain rescue. It has been suggested that Shrug (band) be merged into this article. (Discuss) Proposed since September 2023. Scottish rock band Snow PatrolSnow Patrol performing in 2019Background informationAlso known asShrug (1994–1996)Polarbear (1996–1997)OriginDundee, ScotlandGenres Alternative rock[1] power pop[2] post-Britpop[3] indie rock&...

Municipality in Bagmati Zone, NepalNilkantha नीलकण्ठ नगरपालिकाMunicipalityDhadingbesi HighwayNilkanthaLocation in NepalCoordinates: 27°55′N 84°56′E / 27.91°N 84.94°E / 27.91; 84.94Country NepalZoneBagmati ZoneDistrictDhading DistrictGovernment • TypeMayor–council • MayorMr.Bhim Prasad Dhungana (NC) • Deputy MayorDeepak Bishowkarma(NCP)Population (1991) • Tota...

2006 studio album by Steeleye SpanBloody MenStudio album by Steeleye SpanReleased2006Recorded2006GenreBritish folk rockLength62:52LabelPark RecordsSteeleye Span chronology Winter(2004) Bloody Men(2006) Cogs, Wheels & Lovers(2009) Professional ratingsReview scoresSourceRatingAllmusic [1] Bloody Men is the 20th studio album by British folk rock band Steeleye Span. This album represents a continuation of the band's recent surge of activity. In 2002, the band was in a state of near co...
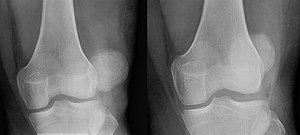
Medical conditionLuxating patellaOther namesTrick knee, subluxation of patella, floating patella, floating kneecapPatellar luxation on radiograph: Left before, right after reduction; after reduction, the patella is still displaced.SpecialtyOrthopedics A luxating patella, sometimes called a trick knee, is a condition in which the patella, or kneecap, dislocates or moves out of its normal location. It can be associated with damage to the anterior cruciate ligament.[1] Patellar luxation ...

Keiner schiebt uns weg Produktionsland Deutschland Originalsprache Deutsch Erscheinungsjahr 2018 Länge 90 Minuten Stab Regie Wolfgang Murnberger Drehbuch Sebastian Orlac,Ulla Ziemann Produktion Katharina M. Trebitsch,Iris Kiefer Musik Michael Beckmann, Tom Stöwer Kamera Peter von Haller Schnitt Florentine Bruck Besetzung Alwara Höfels: Lilli Czipowski Imogen Kogge: Gerda Rapp Katharina Marie Schubert: Rosi Kessler Christoph Bach: Ritschi Blaschke Karsten Antonio Mielke: Kalle Kobel M...



















