Analog signal processing
|
Read other articles:

This article is about the PSP video game. For the Nintendo DS video game, see Bubble Bobble Revolution. 2006 video gameBubble Bobble EvolutionU.S. cover artDeveloper(s)OpusPublisher(s)JP: Marvelous EntertainmentNA: CodemastersPAL: Rising Star Games[1]Platform(s)PlayStation PortableReleaseJP: August 31, 2006EU: September 29, 2006AU: October 19, 2006NA: December 19, 2006Genre(s)Platform, puzzleMode(s)Single-player, multiplayer Bubble Bobble Evolution is a game in the Bubble Bobble serie...

Romanian painter Ion AndreescuIon Andreescu - Self Portrait (1882)Born(1850-02-15)15 February 1850Bucharest, WallachiaDied22 October 1882(1882-10-22) (aged 32)Bucharest, Kingdom of RomaniaResting placeBellu Cemetery, Bucharest, RomaniaNationalityRomanianEducationGheorghe Lazăr Middle SchoolSfântul Sava High SchoolAlma materNational School of Fine ArtsAcadémie JulianKnown forPaintingNotable workThe oakMovementImpressionismParentsAndrei Dobrescu (father)Anastasia Pencovico (mo...

← 1831 1830 1829 1832 في الجزائر → 1833 1834 1835 عقود: فيما يلي قوائم الأحداث التي وقعت خلال عام 1832 في الجزائر. الحكم الإحتلال الفرنسي الأحداث أفريل: مجزرة العوفية (1832) ماي: معركة الحراش (1832) 27 نوفمبر: مبايعة الأمير عبد القادر (1832).[1] المراجع ^ إحياء غدا بمدينة معسكر الذكرى الـ180 لمبايعة �...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ou cette section d'article est rédigé entièrement ou presque entièrement à partir d'une seule source (juillet 2022). N'hésitez pas à modifier cet article pour améliorer sa vérifiabilité en apportant de nouvelles références dans des notes de bas de page. George BeauchampBiographieNaissance 18 mars 1899Comté de Coleman, Texas, États-UnisDécès 30 mars 1941 (à 42 ans)Los Angeles, Cal...

Valleikanaal Lengte 40 km Scheepsklasse niet bevaarbaar Jaar ingebruikname 1941 Van Nederrijn Naar Eem Loopt door Gelderland, Utrecht Het Valleikanaal in Veenendaal Portaal Maritiem Het Valleikanaal in Amersfoort Valleikanaal, Scherpenzeel. Valleikanaal, nabij de Grebbeberg. Het Valleikanaal is een kanaal van ongeveer 40 km lang in de Nederlandse provincies Utrecht en Gelderland. De naam is ontleend aan de Gelderse Vallei, waar het kanaal in noordelijke richting doorhee...

Kim KwonPada tanggal 10 sore, presentasi produksi TV , 2019LahirKim Keon-Woo16 Mei 1989 (umur 34)Korea SelatanPendidikanUniversitas Dongguk – Departmen TeatrePekerjaanAktorTahun aktif2012-sekarangAgen1n1 Stars Nama KoreaHangul김권 Alih AksaraGim GwonMcCune–ReischauerKim KwŏnNama lahirHangul김건우 Alih AksaraGim Geon-uMcCune–ReischauerKim Kŏn-u Kim Kwon (lahir Kim Keon-woo lahir 16 Mei 1989) adalah aktor asal Korea Selatan. Ia tampil dalam beberapa film dan serial televi...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2016. p21 (bahasa Inggris: cyclin-dependent kinase inhibitor 1, CDK-interacting protein 1, p21Waf1/Cip1/Sdi1) merupakan salah satu senyawa penghambat CDK yang memiliki berkas genetik CDKN1A,[1] dan aktivator yaitu faktor transkripsi SREBP-1a.[...

У Вікіпедії є статті про інші значення цього терміна: Жовтяниця. Жовтяниця Chrysosplenium alternifolium Біологічна класифікація Царство: Рослини (Plantae) Клада: Судинні рослини (Tracheophyta) Клада: Покритонасінні (Angiosperms) Клада: Евдикоти (Eudicots) Порядок: Ломикаменецвіті (Saxifragales) Родина: Ломикамен

العلاقات الأردنية الإثيوبية الأردن إثيوبيا الأردن إثيوبيا تعديل مصدري - تعديل العلاقات الأردنية الإثيوبية هي العلاقات الثنائية التي تجمع بين الأردن وإثيوبيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة

Self-portrait Theodore E. Peiser (1853 - 1922) was an early photographer in Seattle, Washington and the Pacific Northwest.[1] His studio and many of his photographs were lost in the Great Seattle Fire of 1889.[2] His surviving photographs include one of the few photographs of the Seattle skyline from Beacon Hill before the fire[3] as well as the Yesler-Leary Building in 1885, several years before it burned in the fire. He also captured the first and second Occidental H...

2004 Indian filmKovilPosterDirected byHariWritten byHariProduced byA. M. RathnamStarringSilambarasanSonia AgarwalCinematographyPriyanEdited byV. T. VijayanMusic byHarris JayarajProductioncompanySri Suriya MoviesRelease date 10 January 2004 (2004-01-10) Running time148 minutesCountryIndiaLanguageTamil Kovil (transl. Temple) is a 2004 Indian Tamil-language romantic drama film written and directed by Hari and produced by A. M. Rathnam. It stars Silambarasan and Sonia Agarwal...

American drama television series PachinkoGenreDramaCreated bySoo HughBased onPachinkoby Min Jin LeeDirected by Kogonada Justin Chon Starring Soji Arai Jin Ha Jun-woo Han In-ji Jeong Eun-chae Jung Min-ha Kim Lee Min-ho Kaho Minami Noh Sang-hyun Anna Sawai Jimmi Simpson Yuh-jung Youn Jeon Yu-na Music byNico MuhlyOpening themeLet's Live for Today by The Grass Roots (English ver.) and Leenalchi (Korean ver.)Country of origin United States[1] Original languages Korean Japanese English No. ...

Georgian politician (1944–1993) Zhiuli Shartavaჟიული შარტავაChairman of the Government of the Autonomous Republic of AbkhaziaIn officeJanuary 11, 1990 – September 27, 1993PresidentZviad GamsakhurdiaHead of the Council of Self-Defence of Autonomous Republic of AbkhaziaIn office1992–1993PresidentEduard Shevardnadze Personal detailsBorn(1944-03-07)March 7, 1944Senaki, Georgian SSR, Soviet UnionDiedSeptember 27, 1993(1993-09-27) (aged 49)Sukhumi, Abkhaz...

Former theatre in Edinburgh, Scotland, UK Palladium TheatreAddressEdinburgh, ScotlandUnited KingdomCoordinates55°56′42″N 3°12′11″W / 55.945°N 3.203°W / 55.945; -3.203ConstructionOpened1886[1]Demolished1984[1] The Palladium Theatre was a theatre at East Fountainbridge in Edinburgh, Scotland.[2] It was originally built as the Royal Circus by John Henry Cooke, opening in 1886.[3] By 1908, it had been converted for use as a cinem...
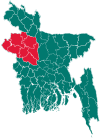
Upazila in Rajshahi Division, BangladeshSanthia সাঁথিয়াUpazilaSanthiaLocation in BangladeshCoordinates: 24°3.5′N 89°32′E / 24.0583°N 89.533°E / 24.0583; 89.533Country BangladeshDivisionRajshahi DivisionDistrictPabna DistrictArea • Total331.56 km2 (128.02 sq mi)Population (1991) • Total283,463 • Density850/km2 (2,200/sq mi)Time zoneUTC+6 (BST)WebsiteOfficial Map of Santhia Santhia...

2003 film by Shawn Levy For other uses, see Just Married (disambiguation). Just MarriedTheatrical release posterDirected byShawn LevyWritten bySam HarperProduced byRobert SimondsLauren Shuler DonnerStarring Ashton Kutcher Brittany Murphy Christian Kane CinematographyJonathan BrownEdited byScott HillDon ZimmermanMusic byChristophe BeckProductioncompanies Mediastream III[1] Robert Simonds Productions[1] Distributed by20th Century FoxRelease date January 10, 2003 (...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (June 2014) (Learn how and when to remove this template message) Hospital in Hong Kong Island, Hong KongTung Wah Eastern HospitalHospital Authority and Tung Wah Group of HospitalsTung Wah Eastern Hospital entranceGeographyLocation19 Eastern Hospital Road, Causeway Bay, Hong Kong Island, Hong KongCoordinates22°16...

1974 novel by Marion Zimmer Bradley The Spell Sword Cover of the first editionAuthorMarion Zimmer BradleyCover artistGeorge BarrCountryUnited StatesLanguageEnglishSeriesDarkoverGenreSword and planetPublisherDAW BooksPublication date1974Media typePrint (paperback)Pages158OCLC156484864Followed byThe Forbidden Tower The Spell Sword is a sword and planet novel by American writer Marion Zimmer Bradley, part of the Darkover series. The book was co-authored by Paul Edwin Zimmer,...

Woodworking shaping and finishing tool For the metalworking handtool, see Hand scraper. This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Card scraper – news · newspapers · books · scholar · JSTOR (April 2020) Card scraper in use A card scraper or cabinet scraper is a woodworking shaping and finishin...

Asosiasi Sepak Bola ThailandAFCDidirikan25 April 1916Bergabung dengan FIFA23 Juni 1925Bergabung dengan AFC1957PresidenWorawi MakudiWebsitewww.fat.or.th Asosiasi Sepak Bola Thailand (bahasa Thai: สมาคมฟุตบอลแห่งประเทศไทย ในพระบรมราชูปถัมภ์) adalah badan pengendali sepak bola di Thailand. Kompetisi Badan ini menyelenggarakan beberapa kompetisi di Thailand, yakni: Liga Utama Thailand Liga Divisi Satu Thailand...







