منظور
|
Read other articles:

Halaman ini berisi artikel tentang perwakilan asing di Indonesia. Untuk daftar perwakilan Indonesia di luar negeri, lihat Daftar perwakilan diplomatik Indonesia. Peta negara-negara di dunia yang memiliki misi diplomatik di Indonesia. Berikut ini adalah daftar perwakilan diplomatik di Indonesia, tidak termasuk konsulat kehormatan. Saat ini, terdapat 104 kedutaan besar di Jakarta. Beberapa negara menugaskan kedutaan besar di ibu kota negara lain merangkap wilayah Indonesia. Kedutaan besar Jakar...

Main article: 1912 United States presidential election 1912 United States presidential election in Iowa ← 1908 November 5, 1912 1916 → Nominee Woodrow Wilson Theodore Roosevelt William Howard Taft Party Democratic Progressive Republican Home state New Jersey New York Ohio Running mate Thomas R. Marshall Hiram Johnson Nicholas M. Butler Electoral vote 13 0 0 Popular vote 185,325 161,819 119,805 Percentage 37.64% 32.87% 24.33% County Results Wils...

Het gebouw in Brussel waar de sterrenwacht van 1834 tot 1890 gevestigd was Koninklijke Sterrenwacht (links) Het Humain Radioastronomy Station[1] logo Koninklijke Sterrenwacht De Koninklijke Sterrenwacht van België werd opgericht in 1826, nog voor het ontstaan van het onafhankelijke België, wanneer Willem I, de koning der Nederlanden, een Koninklijk Besluit ondertekent ter oprichting van een sterrenwacht in Brussel. Initiatiefnemer is de astronoom Adolphe Quételet, die in 1830 tot d...

هذه المقالة عن ولاية المدية. لمعانٍ أخرى، طالع المدية (توضيح). ولاية المدية ولاية المدية الإدارة عاصمة الولاية المدية رمز الولاية 26 ولاية منذ 1962 الموقع الرسمي Medea-dz.com بعض الأرقام مساحة 8866 كم² (22) تعداد السكان 944609 نسمة (13) إحصاء سنة 2008 م كثافة 83.98 نسمة/كم² الترقيم الهاتفي ...

Lake freighter of Canada Steamship Lines Diagram of Kamloops wreckage History Canada NameKamloops OperatorCanada Steamship Lines, Ltd., Montreal, Quebec, Canada BuilderFurness Ship Building Company, Ltd., Stockton-on-Tees, Durham, England, UK Yard number68 Completed1924 FateFoundered off Isle Royale in western Lake Superior 7 December 1927 NotesCanada Registry #147682 General characteristics Class and typePackage freighter – canaller Tonnage 2402 gross 1748 net Length250 ft (76 m)...

Light sponge cake with cream cheese For Japanese no-bake cheesecakes (known as rare cheesecake), see Cheesecake § Asia. Japanese cheesecakeスフレチーズケーキJapanese cheesecake with raspberry jamAlternative namesSoufflé-style cheesecake, cotton cheesecake, light cheesecakeCourseDessertPlace of originJapanCreated byTomotaro KuzunoMain ingredientsCream cheese, butter, sugar, eggs Japanese cheesecake (Japanese: スフレチーズケーキ),[1] also known as soufflé-style...

Indian composer (1903–1981) Raichand Boralরাইচাঁদ বড়ালBoral on a 2013 stamp of IndiaBornRai Chand Boral(1903-10-19)19 October 1903Calcutta, Bengal Presidency, British India (present-day West Bengal, India)[1]Died25 November 1981(1981-11-25) (aged 78)Kolkata, West Bengal, IndiaNationalityIndianOccupationMusic director Rai Chand Boral (19 October 1903 – 25 November 1981) was an Indian composer, considered by music connoisseurs to be the Bhishma Pitamah,...

قرية وادي المعاين - قرية - تقسيم إداري البلد اليمن المحافظة محافظة المحويت المديرية مديرية ملحان العزلة عزلة بني مليك السكان التعداد السكاني 2004 السكان 158 • الذكور 82 • الإناث 76 • عدد الأسر 22 • عدد المساكن 22 معلومات أخرى التوقيت توقيت اليمن (+3 غ�...

Religious makeup of Lahore, Pakistan It is estimated that the city of Lahore, Pakistan, has a Muslim majority with 94.7% and Christian minority constitute 5.1% of the population and rest Sikhs and Hindus constitute the remaining 0.2%. There is also a small but longstanding Zoroastrian community.[1] Religion in Lahore City 2017[2] Religion Percent Islam 94.7% Christianity 5.14% Hinduism 0.02% Sikhism 0.02% Others 0.1% Before Partition Rel...

Grand Prix Spanyol 2023Detail lombaLomba ke 4 dari 20Grand Prix Sepeda Motor musim 2023Tanggal28–30 April 2023Nama resmiGran Premio MotoGP Guru by Gryfyn de EspañaLokasiCircuito de Jerez-Ángel NietoJerez de la Frontera, Cádiz, SpanyolSirkuitFasilitas balapan permanen4.423 km (2.748 mi)MotoGPPole positionPembalap Aleix Espargaró ApriliaCatatan waktu 1:37.216 Putaran tercepatPembalap Francesco Bagnaia DucatiCatatan waktu 1:37.989 di lap 19 PodiumPertama Francesco Bag...

James Morgan Pryse (14 November 1859 – 22 April 1942) was an author, publisher, and theosophist. Emblem of the Theosophical Society Family background Pryse was born in New London, Ohio (a suburb of Cincinnati), and died in Los Angeles, California. Pryse married Jessica 'Jessie' Mayer (died on Aug. 27, 1928) on Dec. 1, 1902 at Galesville, Trempealeau County, Wisconsin. James had a brother named John Morgan Pryse (Sept. 9, 1863 - Sept. 5, 1952)[1] who died in Los Angeles and who w...

Late 18th-century French inventor Tachygraph redirects here. For the device used for recording vehicle data, see Tachograph. Claude ChappeClaude ChappeBorn25 December 1763Brûlon, Sarthe, FranceDied23 January 1805 (1805-01-24) (aged 41)Paris, FranceNationalityFrenchOccupationEngineerEngineering careerProjectssemaphore systemSignificant advancetelecommunications Claude Chappe (French: [klod ʃap]; 25 December 1763 – 23 January 1805) was a French inventor who in 1792 demonst...

MillingenGeneral informationLocationMillingen (Rees), North Rhine-Westphalia GermanyCoordinates51°48′33″N 6°24′02″E / 51.80917°N 6.40056°E / 51.80917; 6.40056Line(s)Arnhem-Oberhausen railwayPlatforms2Tracks2Other informationFare zoneVRR: 793[1]Services Preceding station VIAS Following station Praesttowards Arnhem Centraal RE 19 Empel-Reestowards Düsseldorf Hbf LocationMillingenLocation within North Rhine-Westphalia Millingen (German: Bahnhof M...

Japanese-American mathematician Shizuo Kakutani角谷 静夫Kakutani in 1970Born(1911-08-28)August 28, 1911Osaka, JapanDiedAugust 17, 2004(2004-08-17) (aged 92)New Haven, Connecticut, USNationalityJapanese AmericanAlma materTohoku UniversityKnown forKakutani fixed-point theoremMarkov–Kakutani fixed-point theoremKakutani's theorem (geometry)Kakutani–Rokhlin lemmaRiesz–Markov–Kakutani representation theoremSpouseKeiko (Kay) UchidaChildrenMichiko KakutaniScientific careerF...

1919 silent film by David Smith A Fighting ColleenLobby cardDirected byDavid SmithScreenplay byGerald C. Duffy[1]Story byGerald C. Duffy[1]Starring Bessie Love Charles Spere CinematographyCharles R. Seeling[2]ProductioncompanyVitagraph Company of America[1]Release date November 16, 1919 (1919-11-16) (U.S.)[3][4] Running time5 reels;[1] 4,471 feet[5]CountryUnited StatesLanguageSilent (English intertitles) A Figh...

Original video animation Labyrinth of FlamesOfficial Region 1 DVD Cover released by Central Park Media炎のらびりんす(Honō no Rabirinsu)GenreAction, comedy, romance[1][2] Original video animationDirected byKatsuhiko NishijimaProduced byKiyoshi SugiyamaShigeo Kaneko (#2)Written byKatsuhiko NishijimaKenichi KanemakiMusic byKouichi FujinoStudioStudio FantasiaLicensed byNA: Central Park MediaReleased September 25, 2000 – December 21, 2000Episodes2...

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada.Este aviso fue puesto el 30 de marzo de 2020. Derechos LGBT en Corea del SurBanderaEscudo HomosexualidadEs legal Edad de consentimiento sexualHeterosexual y homosexual igual Edad de consentimiento homosexual 16Protección legal contra la discriminaciónLaboral / (En algunas jurisdicciones, propuesto a nivel nacional)Bienes y servicios / (En algunas jurisdicciones, propuesto a nivel nacional)En todos lo...

Location of Susquehanna County in Pennsylvania This is a list of the National Register of Historic Places listings in Susquehanna County, Pennsylvania. This is intended to be a complete list of the properties on the National Register of Historic Places in Susquehanna County, Pennsylvania, United States. The locations of National Register properties for which the latitude and longitude coordinates are included below, may be seen in a map.[1] There are eight properties listed on the Nat...

Indian diplomat Suresh K. ReddyAmbassador Suresh Reddy on 19 February 2021Ambassador of India to the Federative Republic of BrazilIn office13 September 2020 – 26 July 2022PresidentRam Nath KovindSucceeded byAshok Das[1] Personal detailsNationalityIndianResidence(s)Brasilia, BrazilAlma materJawaharlal Nehru UniversityOccupationDiplomat Suresh K Reddy is an Indian diplomat and current Ambassador of India to Brazil.[2] He previously served as ambassador to ASEAN, Iraq,...

This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (May 2015) Human settlement in ScotlandLesmahagowScottish Gaelic: Lios MoChudaScots: Lismahagie or The GowLesmahagowLocation within South LanarkshirePopulation4,300 (mid-2020 est.)[1]OS grid referenceNS8139• Edinburgh35.8 miles (57.6 km)• London324 miles ...









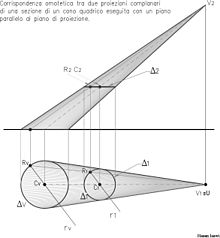



![خط الافق, في هذا النوع من المنظور، يتطابق مع خط الارض ولذلك يسمى "منظور عين النملة"[6]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/18/%D9%85%D9%86%D8%B8%D9%88%D8%B1_%D8%B9%D9%8A%D9%86_%D8%A7%D9%84%D9%86%D9%85%D9%84%D8%A9.jpg/120px-%D9%85%D9%86%D8%B8%D9%88%D8%B1_%D8%B9%D9%8A%D9%86_%D8%A7%D9%84%D9%86%D9%85%D9%84%D8%A9.jpg)
![إعادة تأهيل زاوية من المنزل باستخدام قواعد المنظور.[7]](http://upload.wikimedia.org/wikipedia/commons/thumb/c/c1/Elaborazione-prospettica.jpg/120px-Elaborazione-prospettica.jpg)