معادلة أفرامي
|
Read other articles:

Mercury(II) thiocyanate Names Other names Mercuric thiocyanateMercuric sulfocyanate Identifiers CAS Number 592-85-8 Y 3D model (JSmol) Interactive image ECHA InfoCard 100.008.886 EC Number 209-773-0 PubChem CID 11615 UNII 3JNH1DM7IF Y CompTox Dashboard (EPA) DTXSID7060469 InChI InChI=1S/2CHNS.Hg/c2*2-1-3;/h2*3H;/q;;+2/p-2Key: GBZANUMDJPCQHY-UHFFFAOYSA-L SMILES C(#N)[S-].C(#N)[S-].[Hg+2] Properties Chemical formula Hg(SCN)2 Molar mass 316.755 g/mol Appearance ...

مزرعاوي - قرية - تقسيم إداري البلد إيران[1] المحافظة محافظة خوزستان المقاطعة مقاطعة الفلاحية قسم القسم المركزي القسم الريفي قسم حسيني الريفي إحداثيات 30°42′21″N 48°43′16″E / 30.70583°N 48.72111°E / 30.70583; 48.72111 السكان التعداد السكاني 62 نسمة (إحصاء 2016) معلومات

イオン福重店ÆON FUKUSHIGE 地図 店舗概要所在地 〒819-0041福岡県福岡市西区拾六町1丁目7番1号座標 北緯33度34分2秒 東経130度18分53秒 / 北緯33.56722度 東経130.31472度 / 33.56722; 130.31472 (イオン福重店)座標: 北緯33度34分2秒 東経130度18分53秒 / 北緯33.56722度 東経130.31472度 / 33.56722; 130.31472 (イオン福重店)開業日 1983年11月23日(福重アピロス)

Questa voce sugli argomenti aeroporti della Russia e Cabardino-Balcaria è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Aeroporto di Nal'čikaeroporto Codice IATANAL-НЧК Codice ICAOURMN-УРМН Nome commercialeAeroporto di Nal'čikАэропорт Нальчик DescrizioneTipoCivile, militare GestoreElbrus-Avia Stato Russia Circondario federale Cabardino-Balcaria Posizionea 3 km a nord-est dal centro di Nal'čik Altitudine432 m ...

Das Zugbeeinflussungssystem S-Bahn Berlin (ZBS) ist ein seit 2011 zum Einsatz kommendes, eigenständiges Zugbeeinflussungssystem, das von der DB Netz AG, der S-Bahn Berlin GmbH und Siemens Transportation Systems in Braunschweig entwickelt wurde. Das ZBS dient der Überwachung des Fahr- und Bremsverhaltens des Triebfahrzeugführers bei Zug- und Rangierfahrten auf Strecken der S-Bahn Berlin. Es handelt sich um ein verdeckt arbeitendes punktförmiges Zugbeeinflussungssystem mit kontinuierlicher ...

1993 album This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Who Covers Who? – news · newspapers · books · scholar · JSTOR (September 2016) (Learn how and wh...

SaeroenLahirYogyakarta, Hindia BelandaMeninggal06 Oktober 1962Bogor, IndonesiaKebangsaanIndonesiaNama lainKampret (nama pena)PekerjaanJurnalis, penulis skenarioKarya terkenalTerang Boelan Saeroen (Ejaan Yang Disempurnakan: Saerun; fl. 1920an–1962) adalah jurnalis dan penulis skenarion asal Indonesia. Ia lahir di Yogyakarta, ia menjadi jurnalis setelah waktu kerja di stasiun kereta api. Pada pertengahan tahun 1930-an ia mendirikan koran harian Pemandangan dengan Raden Haji Djunaedi dan ...

Chen AisenChen Aisen dan Lin Yue pada Olimpiade Rio 2016Informasi pribadiNama asli陈艾森KewarganegaraanTiongkokLahir22 Oktober 1995 (umur 28)Guangzhou, TiongkokTinggi168 m (551 ft 2 in)Berat60 kg (132 pon) OlahragaNegaraTiongkokOlahragaLoncat indahLomba10 m, 10 m synchroKlubProvinsi Guangdong Rekam medali Loncat indah putra Mewakili Tiongkok Turnamen 1 2 3 Permainan Olimpiade 2 1 0 Kejuaraan Dunia 3 1 0 Piala Dunia Loncat Indah FINA 3 1 0 Total 8 3 0 Oli...

Kekaisaran Persia AkhemeniyahParsāsek. 550 SM–336 SM Lambang Koresy Agung Lambang Wilayah terluas Kekaisaran Akhemeniyah di bawah Darius I.StatusKekaisaranIbu kotaPasargadae, Ekbatana, Parsa, Susa, BabilonBahasa yang umum digunakanBahasa Persia Kuno (bahasa asli)bahasa Aram Kekaisaran (Bahasa resmi dan basantara)[1]bahasa Elambahasa Akkadia[2]Agama ZoroastrianismePemerintahanMonarkiSyah • 559–529 SM (pertama) Koresy Agung• 336–330 SM (terakhir) D...

13th-century Danish scholar Page from Modi significandi by Martinus de Dacia Martin of Dacia (Martinus Dacus, Martinus de Dacia, Morten Mogensen, c. 1240 - 10 August 1304) was a Danish scholar and theologian. He authored De Modi significandi (ca. 1270), an influential treatise on grammar. [1] [2] Biography Morten Mogensen was born at Ribe in Jutland probably in the late 1240s or early 1250s. Mogensen received his theological doctorate in Paris where he obtained the degree of a...

Amtrak service between San Jose and Auburn, California Amtrak Capitols redirects here. For the Amtrak line connecting Washington, D.C. and Chicago, see Capitol Limited (Amtrak train). Capitol CorridorA Capitol Corridor train in Pinole, California, in 2011OverviewService typeInter-city rail, commuter railLocaleNorthern CaliforniaFirst serviceDecember 12, 1991; 31 years ago (1991-12-12)Current operator(s)Capitol Corridor Joint Powers Authority, in partnership with Amtrak and C...

Deutsche Schule La Paz (Spanish: Colegio Alemán Mariscal Braun) is a German international school in La Paz, Bolivia.[1] The school serves Kindergarten through grade 12 (Sekundarstufe/Secundaria 12). The school was founded on 10 May 1923.[2] See also Ethnic Germans in Bolivia References ^ Kontakt. Deutsche Schule La Paz. Retrieved on 23 March 2015. Avenida Alexander # 100 Achumani Casilla 605 – 4442 La Paz, Bolivien ^ Geschichte (Archive) / Historia (Archive). Deutsche Schul...

For the former video game, see Cookie Run. American food reality television pilot Cookie WarsGenreFood reality televisionPresented byJonathan BennettJudges Shinmin Li Andi Kirkegaard[1] Country of originUnited StatesProductionRunning time41:00Production companySuper Delicious[2]Original releaseNetworkFood NetworkReleaseDecember 22, 2019 (2019-12-22)[2][3] Cookie Wars is an American cooking competition television pilot that aired on Food Network o...

French TV series or program The Desert ForgesCreated byPierre SportolaroBased onLes Forges du DésertPresented byRichard FairbrassGabrielle RichensStarringMelanie Winiger as The PoetessCountry of originFranceNo. of series1No. of episodes10ProductionRunning time60 minutes (inc. adverts)Production companiesGrundy and Adventure Line ProductionsOriginal releaseNetworkChannel 5Release23 June (2001-06-23) –25 August 2001 (2001-08-25)RelatedFort BoyardThe Crystal Maze The Deser...

Canadian-American astrophysicist and cosmologist For the American football player, see Jim Peebles (American football). For the Australian rugby league player, see Jim Peebles (rugby league). Jim PeeblesCC OM FRSPeebles in 2010BornPhillip James Edwin Peebles (1935-04-25) April 25, 1935 (age 88)Winnipeg, Manitoba, CanadaNationalityCanadian, AmericanEducationUniversity of Manitoba (BS)Princeton University (MS, PhD)Known forCosmic microwave background radiationCosmic infrared b...

2014 soundtrack album by Mick GordonWolfenstein: The New Order (Original Game Soundtrack)Soundtrack album by Mick GordonReleasedMay 19, 2014GenreSoundtrack, Industrial rock, Heavy metalLength51:45LabelBethesda Softworks Wolfenstein: The New Order (Original Game Soundtrack) is the soundtrack to the video game Wolfenstein: The New Order. The soundtrack was released on 19 May 2014, consisting of an original score featured in the game.[1] Composer Mick Gordon took inspiration from...

Терена Современное самоназвание Terena[1] Численность 19 000 Расселение Бразилия Язык терена Религия анимизм[уточнить] Медиафайлы на Викискладе Девочка из племени терена Терена, также терено, этелена — аборигенный народ в Бразилии. Численность к началу XXI ве...
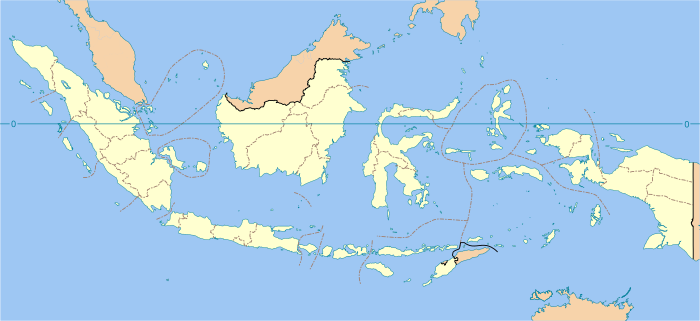
Untuk pandemi yang sedang berlangsung di Indonesia, lihat pandemi COVID-19 di Indonesia. Berdasarkan Keputusan Menteri Kesehatan Republik Indonesia Nomor HK.01.07/MENKES/169/2020, berikut daftar rumah sakit rujukan penanggulangan penyakit infeksi emerging tertentu (termasuk COVID-19) berdasarkan provinsi.[1] Aceh SumatraUtara SumatraBarat Riau KepRiau Bengkulu Sumatera Selatan Lampung Kep. BangkaBelitung Jambi Banten Jakarta JawaBarat JawaTengah Yogyakarta JawaTimur KalimantanBarat Ka...

Trico Plant No. 1 Thanks for expanding Trico Plant No. 1. Unbelievable they would conceive of tearing this down! Such an important piece of our industrial heritage. bastards.--Pubdog (talk) 01:44, 20 March 2012 (UTC)Reply[reply] A barnstar for you! The Original Barnstar for a brilliant and timely expansion of the Trico Plant No. 1 stub Pubdog (talk) 01:46, 20 March 2012 (UTC)Reply[reply] ArbCom 2020 Elections voter message Hello! Voting in the 2020 Arbitration Committee elections is ...

安住の地を求めてポーランドにやってきたユダヤ人の集団(1096年)を暖かく迎え、国内定住の許可を与えるポーランド公ヴワディスワフ1世ヘルマン(公の座に掛けている、冠と杖と赤マントの人物)とその一人息子で父から二代後にポーランド公となる、当時11歳のボレスワフ3世クシヴォウスティ(中央の、両手で杖を持って立っている、冠と赤マントの少年)、そし...



















![{\displaystyle Y=1-\exp[-K(t)^{n}]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c9454721e5f665e4e8ec46fda65793398473104)


![{\displaystyle \ln \,{(-\ln {[1-Y(t)]})}=\ln K+n\ln t\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d35a8142913d6b7d5ef5f024855011a58e668cf7)











