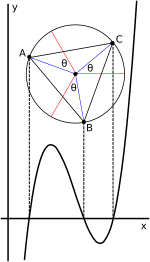
معادلة تكعيبية

  ميّز عن دالة تكعيبية.

منحنى دالة تكعيبية بثلاث جذور حقيقية (حيث يلتقي المنحنى بمحور الأفاصيل المعرف ب y = 0). المنحنى المبين هنا له نقطتان حرجتان. الدالة التي تعرف هذا المنحنى هي f(x) = (x³ + 3x² − 6x − 8)/4.

في الجبر، معادلة تكعيبية (بالإنجليزية: Cubic equation)‏ ذات متغير واحد هي معادلة تأخذ الشكل التالي :

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

حيث مختلف عن الصفر العددُ a.

حل المعادلة التكعيبية يعني ايجاد جذور الدالة التكعيبية وهو ليس بالأمر السهل كما في معادلة الدرجة الثانية. وصل الأمر بالعلماء إلى أن اعتقدو بأنه ليس لهؤلاء المعادلات من حلحلة.

يمكن إثبات القانون العام لجذور معادلة الدرجة الثالثة باستخدام صيغة كاردانو أو باستعمال الحساب المثلثي أو باستعمال التحليل العددي وبالتحديد خوارزميات إيجاد جذور دالة، طريقة نيوتن مثالا على ذلك.

التاريخ

كانت الدوال التكعيبية معروفة لدى البابليين القدامى والإغريق والصينيين والهنديين والمصريين.

انظر إلى مضاعفة المكعب.

في القرن الحادي عشر، قام عالم الرياضيات والشاعر الفارسي عمر الخيام (1048-1131) بتطورات مهمة في نظرية المعادلات التكعيبية، حيث برهن على إمكانية وجود أكثر من حل لمعادلة تكعيبية ما.

في القرن الثاني عشر، حاول عالم الرياضيات الهندي باسكارا حل المعادلة التكعيبية ولكن محاولته باءت بالفشل. ولكنه أعطى المثال x³ + 12x = 6x² + 35 عن هؤلاء المعادلات.

في القرن الثاني عشر ذاته كتب عالم الرياضيات الفارسي شرف الدين الطوسي (1135-1213) كتابا سماه المعادلات، تطرق فيه إلى ثمانية أنواع من المعادلات التكعيبية ذات جذور موجبة وخمسة أنواع أخرى قد لا يكون لها جذور موجبة. استعمل من أجل ذلك ما أطلق عليه فيما بعد اسم طريقة روفيني-هورنر الممكنة من الاقتراب من جذور المعادلة حسابيا.

استطاع ليوناردو فيبوناتشي (1170-1250) في كتاب له أن يقترب من الحلول الموجبة للمعادلة x³ + 2x² + 10x = 20 إلى حدود خطأ صغير جدا يُقدر بحوالي 10⁻⁹.^[1]

في بداية القرن السادس عشر، وجد عالم الرياضيات الإيطالي سيبيوني ديل فيرو (1465-1526) طريقة لحل المعادلات من الدرجة الثالثة من صنف خاص هو x³ + mx = n. فعليا، جميع المعادلات التكعيبية يمكن أن تُحول إلى هذا الشكل شرط أن يُقبل كون العددين m و n سالبين، ولكن الأعداد السالبة لم تكن معروفة لدى ديل فيرو في ذلك الزمان. يضاف إلى ذلك أن ديل فيرو ترك اكتشافه هذا سريا إلى حدود قُبيل وفاته، مخبرا بها تلميذا له يسمى أنطونيو فيور.

في عام 1539، أقنع جيرولامو كاردانو (1501-1576)، تارتاغليا أن يفشي له بسره حول المعادلات التكعيبية، شرط أن يمتنع كاردانو عن نشر هذه الحلحلة، وأن يعطيه الوقت أن ينشر هو هذا العمل. سنوات بعد ذلك، علم كاردانو بعمل ديل فيرو الذي سبق عمل تارتاغليا، فنشر طريقة ديل فيرو في كتاب لع عام 1545 عنوانه أرس ماغنا، معطيا بذلك لتارتاغليا فترة زمنية تقدر بست سنوات.

أشار كاردانو أن طريقة تارتاغليا قد تتطلب منه في بعض الأحيان اعتبار الجذور التربيعية للأعداد السالبة. كان ذلك أول بداية لظهور الأعداد المركبة. درس رافائيل بومبيلي هذه المسألة بدقة ليصبح عادة بذلك المكتشف الفعلي للأعداد المركبة

تمكن فرانسوا فييت (1540-1603) بشكل مستقل من ايجاد الحل باستعمال الحساب المثلثي لمعادلة تكعيبية جذورها أعداد حقيقية. أتم عملَ فييت وعممه العالم رينيه ديكارت (1596-1650).

نيكولو فونتانا تارتاغليا، أحد عالمي الرياضيات الإيطاليين اللذان حلا المعادلات التكعيبية

المعادلات التكعيبية المبسطة

المعادلات التكعيبية المبسطة وقد تسمى المعادلات التكعيبية منخفضة الضغط هي معادلات تكعيبية تكتب على الشكل التالي.

${\displaystyle x^{3}+px+q}$

تغيير بسيط للمتغير يمكن من المرور من معادلة تكعيبية في شكلها العام إلى شكلها المبسط.

لتكن المعادلة التكعيبية التالية

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

تغيير المتغير

${\displaystyle x=t-{\frac {b}{3a}}}$

يعطي معادلة تكعيبية معاملها منعدم في حدها t². بعد القسمة على a يُحصل على المعادلة التكعيبية منخفضة الضغط

${\displaystyle t^{3}+pt+q=0,}$

حيث

${\displaystyle {\begin{aligned}t=&x+{\frac {b}{3a}}\\p=&{\frac {3ac-b^{2}}{3a^{2}}}\\q=&{\frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}}.\end{aligned}}}$

جذور المعادلة الأصلية ${\displaystyle x_{1},x_{2},x_{3}}$ ترتبط بجذور المعادلة المبسطة ${\displaystyle t_{1},t_{2},t_{3}}$ بالعلاقة

${\displaystyle x_{i}=t_{i}-{\frac {b}{3a}},}$

حيث ${\displaystyle i=1,2,3}$.

طبيعة جذور معادلة تكعيبية وحساب المميز

جذور معادلة تكعيبية تدخلن في إطار حالتين اثنتين لا ثالث لهما.

• الحالة الأولى هي أن يكون الجذر الأول حقيقيا والجذران الآخران عددين عقديين، الواحد منهما هو مرافق الثاني.
• الحالة الثانية هي أن تكون الجذور الثلاثة كلهن حقيقية. وقد تتساوى مع بعضهن البعض وقد تختلف عن بعضهن البعض.

حالة جذرين حقيقيين وجذر ثالث عقدي حالة غير ممكنة للسبب التالي :

إذا كان ${\displaystyle z}$ حلحلة لمعادلة تكعيبية ما فإن ${\displaystyle {\overline {z}}}$ هو أيضا حلحلة لهذه المعادلة، وإذا كان ${\displaystyle z}$ غير حقيقي فإن ${\displaystyle {\overline {z}}}$ هو أيضا غير حقيقي.

الحلحلة الجبرية

تعطى الصيغة العامة لجذور معادلة الدرجة الثالثة ${\displaystyle ax^{3}+bx^{2}+cx+d=0\,}$ بدلالة معاملاتها ${\displaystyle a,b,c,d\,}$ كما يلي:

المميز

عدد جذور دالة تكعيبية الحقيقية والمركبة يحدد بحساب مميز المعادلة التكعيبية كما يلي:

${\displaystyle \Delta =18abcd-4b^{3}d+b^{2}c^{2}-4ac^{3}-27a^{2}d^{2}.}$

• إذا كان Δ > 0، فإن للمعادلة ثلاثة جذور مختلفة الواحدة منها عن الأخريين.
• إذا كان Δ = 0، فإن للمعادلة جذرا متكررا وأن جميع حلول المعادلة حقيقية.
• إذا كان Δ < 0، فإن للمعادلة جذرا حقيقيا وجذرين أخريين مركبين الواحد منهما مرافق للآخر.

تعطى الصيغة العامة لجذور معادلة الدرجة الثالثة، ${\displaystyle ax^{3}+bx^{2}+cx+d=0\,}$ بدلالة معاملاتها ${\displaystyle a,b,c,d\,}$ كما يلي:

${\displaystyle {\begin{aligned}x_{1}=&-{\frac {b}{3a}}\\&-{\frac {1}{3a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d+{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\\&-{\frac {1}{3a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d-{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\\x_{2}=&-{\frac {b}{3a}}\\&+{\frac {1+i{\sqrt {3}}}{6a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d+{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\\&+{\frac {1-i{\sqrt {3}}}{6a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d-{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\\x_{3}=&-{\frac {b}{3a}}\\&+{\frac {1-i{\sqrt {3}}}{6a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d+{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\\&+{\frac {1+i{\sqrt {3}}}{6a}}{\sqrt[{3}]{\frac {2b^{3}-9abc+27a^{2}d-{\sqrt {\left(2b^{3}-9abc+27a^{2}d\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}{2}}}\end{aligned}}}$

صيغة كاردانو

كاردانو هو عالم رياضيات وفيزيائي وفلكي إيطالي. نشر هذه الصيغة في كتابه أرس ماغنا عام 1545 م.

تقتضي الطريقة :

• أولا تبسيط المعادلة القياسية لتصبح على الشكل

${\displaystyle x^{3}+ax^{2}+bx+c=0\qquad (1)}$. قد يسمى هذا الشكل من الحدوديات متعددات حدود واحدية المدخل.

• ثم التخلص من معامل الدرجة الثانية باستخدام التعويض المناسب ${\displaystyle x=t-a/3\,}$ لتصبح المعادلة بالشكل الجديد:

${\displaystyle t^{3}+pt+q=0\,\qquad (2)}$

حيث

${\displaystyle p=-{\frac {a^{2}}{3}}+b\qquad {\mbox{و}}\qquad q={\frac {2a^{3}}{27}}-{\frac {ab}{3}}+c}$

• وبتعويض مناسب :${\displaystyle t=u+v\,}$ في المعادلة (2) يمكن الحصول على:

${\displaystyle u^{3}+v^{3}+(3uv+p)(u+v)+q=0\qquad (3)\,}$.

• وهنا افترض كاردان حدا جديدا للمتغيرات u وv بحيث ${\displaystyle 3uv+p=0\,}$
• عند دمج هذه في (3) بتعويض v نحصل على:

${\displaystyle u^{6}+qu^{3}-{p^{3} \over 27}=0\,.}$

• هذه معادلة من الدرجة السادسة يمكن أن تبسط إلى الدرجة الثانية في u³ وتحل مباشرة. مميزها هو ${\displaystyle \Delta ={{4p^{3}+27q^{2}} \over 27}}$. دراسة إشارة هذا المميز تعطي ثلاث حالات.

Δ موجب قطعا

${\displaystyle u^{3}=-{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}$

${\displaystyle v^{3}=-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}$

وبالتالي:

${\displaystyle u={\sqrt[{3}]{-{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}\qquad (4)}$

${\displaystyle v={\sqrt[{3}]{-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}\qquad (4)}$

الحل الحقيقي الوحيد هو ${\displaystyle t_{1}=u+v}$.

و حلان عقديان مترافقان:

• ${\displaystyle t_{2}=ju+{\bar {j}}v}$
• ${\displaystyle t_{3}={\bar {j}}u+jv}$

حيث ${\displaystyle j=-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}=e^{i{\frac {2\pi }{3}}}}$

Δ سالب قطعا

يوجد عدد عقدي u الذي هو جذر مكعب ل ${\displaystyle {\frac {-27q+3i{\sqrt {3}}{\sqrt {-\Delta }}}{2}}}$.

المعادلة تقبل ثلاث حلول حقيقية:

• ${\displaystyle x_{1}={\frac {1}{3}}(u+{\bar {u}})}$
• ${\displaystyle x_{2}={\frac {1}{3}}(ju+{\bar {j}}{\bar {u}})}$
• ${\displaystyle x_{3}={\frac {1}{3}}(j^{2}u+{\bar {j^{2}}}{\bar {u}})}$

انظر إلى حالة غير قابلة للتبسيط (معادلات تكعيبية).

• ولما كانت t = v + u, t = x + a/3, وv = −p/3u, نجد

أن:

${\displaystyle x=-{\frac {p}{3u}}+u-{a \over 3}.}$

لاحظ أنه يوجد ثلاث حالات لحساب u في (4) وثلاث حالات لحساب v. ذلك لأن الجذر التكعيبي يحمل ثلاث احتمالات.

أولا، إذا كانت p = q = 0, فإنه لدينا ثلاثة جذور حقيقية

${\displaystyle t=0.\,}$

ثانيا، إذا كانت p = 0 وq ≠ 0, فإن:

${\displaystyle u=0{\text{ و }}v=-{\sqrt[{3}]{q}}.}$

ثالثا إذا كانت p ≠ 0 وq = 0 فإن:

${\displaystyle u={\sqrt {p \over 3}}\qquad {\mbox{و}}\qquad v=-{\sqrt {p \over 3}},}$

وفي أي من الحالات تكون الجذور الثلاثة هي:

${\displaystyle t=u+v=0,\qquad t=\omega _{1}u-{p \over 3\omega _{1}u}={\sqrt {-p}},\qquad t={u \over \omega _{1}}-{\omega _{1}p \over 3u}=-{\sqrt {-p}},}$

حيث

${\displaystyle \omega _{1}=e^{i{\frac {2\pi }{3}}}=-{\tfrac {1}{2}}+i{\tfrac {\sqrt {3}}{2}}.}$

طريقة كاردان هي طريقة تمكن من حل جميع المعادلات من الدرجة الثالثة.

هذه الطريقة تكمن من استعمال صيغ كاردان المعطاة بدلالة ${\displaystyle {\mathcal {}}p}$ و${\displaystyle {\mathcal {}}q}$ حلول المعادلة: ${\displaystyle {\mathcal {}}x^{3}+px+q=0~}$. وهي تمكن من البرهنة على أن المعادلات من الدرجة 3 يمكن حلها جبريا.

Δ مساو للصفر

قد تدمج هذه الحالة في حالة المميز الموجب. وقد تدمج أيضا في حالة الميز السالب. النتيجة لا تتغير. بتعويض Δ بقيمته المساوية للصفر في المعادلات السابقة الذكر، يصير للمعادلة حلا حقيقيا بسيطا هو ${\displaystyle t1=2*u=2{\sqrt[{3}]{-{\tfrac {q}{2}}}}}$ وحل حقيقيا مزدوجا هو ${\displaystyle t2=-u=-{\sqrt[{3}]{-{\tfrac {q}{2}}}}}$.

الصيغة العامة

يمكن استنتاج الصيغة التكعيبية لجذور المعادلة التكعيبية العامة (مع a ≠ 0):

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$ من كل شكل من أشكال صيغة كاردانو عن طريق الاختزال إلى شكل تكعيبي مبسط.

الصيغة معقدة إلى حد ما، يجدر تقسيمها إلى صيغ أصغر.

لتكن

${\displaystyle {\begin{aligned}\Delta _{0}&=b^{2}-3ac,\\\Delta _{1}&=2b^{3}-9abc+27a^{2}d,\end{aligned}}}$

و

${\displaystyle C={\sqrt[{3}]{\frac {\Delta _{1}\pm {\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}}{2}}},}$

حيث يشير الرمز ${\displaystyle {\sqrt[{3}]{{~}^{~}}}}$ إلى جذر تكعيبي لعدد ما.

الإشارة "±" قبل الجذر التربيعي تعني إما "+" أو "-"؛ الخيار قد يكون اختيارياً، وتغييره يؤدي إلى تغيير الجذر التربيعي. ومع ذلك، إذا أدى أحد الخيارات إلى C = 0، فيجب تحديد الإشارة الأخرى. ثم، أحد الجذور هي:

${\displaystyle x=-{\frac {1}{3a}}\left(b+C+{\frac {\Delta _{0}}{C}}\right){\text{.}}}$

يمكن الحصول على الجذرين الآخرين عن طريق تغيير اختيار الجذر التكعيبي في تعريف C، أو مكافئًا بضرب C في الجذر التكعيبي للوحدة البدائي، أي –1 ± i√3/2. وبعبارة أخرى، فإن الجذور الثلاثة هي:

${\displaystyle x_{k}=-{\frac {1}{3a}}\left(b+\xi ^{k}C+{\frac {\Delta _{0}}{\xi ^{k}C}}\right),\qquad k\in \{0,1,2\}{\text{,}}}$

حيث ξ = –1 + i√3/2.

الحلحلة الهندسية

حلحلة عمر الخيام

الحل الهندسي لمعادلة تكعيبية، قام به عمر الخيام عندما يتوفر m = 2 n = 16، موجدا الجذر 2. تقاطع المستقيم العمودي مع محور الأفاصيل يعطي حل للمعادلة.

من أجل حل المعادلة x³ + m²x = n حيث n > 0، أنشأ عمر الخيام قطعا مكافئا^{[ملاحظة 1]} معادلته y = x²/m وأنشأ دائرة قطرها القطعة [0, n/m²]، مرسوما على محور السينات.^{[ملاحظة 2]} بعد ذلك رسم المستقيم العمودي الذي يمر من تقاطع الدائرة والقطع المكافئ. حل المعادلة هو المسافة بين أصل المعلم وتقاطع هذا المستقيم العمودي مع محور السينات. انظر الشكل وبالتحديد إلى القطعة الأفقية الحمراء على محور الأفاصيل.

التفسير الهندسي لجذور دالة تكعيبية

حالة ثلاث جذور حقيقية

بالنسبة إلى معادلة تعكيبية ذات ثلاث جذور حقيقية، الجذور هي إسقاطات على محور الأفاصيل للرؤوس الثلاث لمثلث متساوي الأضلاع، رُسم على دائرة مركزها له نفس أفصول نقطة انعطاف هذه الدالة التكعيبية.

${\displaystyle t_{k}=2{\sqrt {-{\frac {p}{3}}}}\cos \left({\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-k{\frac {2\pi }{3}}\right)}$

حيث ${\displaystyle k=0,1,2}$

تطبيقات

في الرياضيات

• تثليث زاوية ومضاعفة المكعب معضلتان قديمتان في الهندسة، بُرهن على استحالة حلحلتهما باستعمال المسطرة والفرجار لأنها يكافئان حلحلة المعادلات من الدرجة الثالثة.
• جيب التمام لثُلث زاوية، حيث جيب التمام لهذه الزاوية ذاتها معلوم، هو حلحلة لمعادلة تكعيبية. تبقى هذا الخاصية صحيحة إذا بُدل الجيب التمام بدالة مثلثية أخرى.

في العلوم الأخرى

انظر إلى معادلة شارلوت ^{[الإنجليزية]} في الكيمياء.

انظر أيضًا

• معادلة من الدرجة الأولى
• معادلة حدودية
• التكامل الوظيفي

هوامش وملاحظات

1. يسمى أيضًا "شلجم".
2. يسمى أيضا محور الفواصل أو محور الأفاصيل

مراجع

1. O'Connor، John J.؛ Robertson، Edmund F.، "Fibonacci"، تاريخ ماكتوتور لأرشيف الرياضيات

وصلات خارجية

• طريقة كاردانو لحل المعادلات التكعيبية على شبكة الرياضيات رمز