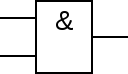
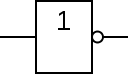
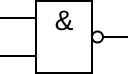
بوابة منطقية
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Australian politician (1945–2021) Carmel Maude Holmes (5 December 1945 – 7 November 2021) was an Australian politician. Carmel Holmes - 1984 Holmes was born in Winnaleah, a small country town in the North East of Tasmania where her parents and grand parents farmed and ran a dairy herd. She attended St Thomas More's Ladies College in Launceston. At the age of 19 she started a recruitment business. In 1976 Carmel Clark married Charles Holmes and in 1978 they moved from Launceston to Hobart ...
هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. نساء من مصر القديمة تعود ل 400 فبل الميلاد-قبر طيبة. يفترض علماء الإناسة (انثروبولوجيا) منطقيا أن البشر يعيشون أصلا عراة، دون ملابس، كوضع طبيعي وأن تكييف جلود الحيوانات والنباتا

Флагман ІІ рангу РСЧФ СРСР Нашивки Радянські військові звання Існування 1935-1940 Категорія звань Вищій командний склад НАТОеквівалент Сухопутні війська/ВПС Комдив Політичний склад Дивізійний комісар Фла́гман ІІ ра́нгу (нід. vlagman, від нід. vlag — прапор та нід. man — людин...

Ten artykuł dotyczy 51 Pułku Piechoty II RP. Zobacz też: 51 Pułk Piechoty - inne pułki piechoty z numerem 51. 51 pułk piechotyStrzelców Kresowych9 pułk strzelców pieszych Odznaka pamiątkowa 51 pp Historia Państwo Polska Sformowanie 1919 Rozformowanie 1939 Nazwa wyróżniająca Strzelców Kresowych Tradycje Święto 27 maja[a] Nadanie sztandaru 28 maja 1928 Rodowód 3 pp im. Garibaldiego9 pułk strzelców polskich9 pułk strzelców pieszych Kontynuacja 12 Brygada Zmechanizowan...

Map all coordinates using: OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) Canada and the United States have one land dispute over Machias Seal Island (off the coast of Maine), and four other maritime disputes in the Arctic and Pacific. Although they share the longest international border in the world, the two countries have a long history of disputes about the border's demarcation (see Canada–United States border).[...

Hanno und Ilse Hahn im April 1960 in Ostia Antica Hanno Hahn (* 9. April 1922 in Berlin-Dahlem; † 29. August 1960 in Mars-la-Tour, Frankreich) war ein deutscher Kunsthistoriker und Architekturforscher. Die Entdeckung der Proportionsgesetze der Zisterzienser-Baukunst im 12. Jahrhundert machte ihn in Fachkreisen weltweit bekannt. Inhaltsverzeichnis 1 Biographie 1.1 Herkunft 1.2 Beginn des Studiums, Kriegseinsatz, Heirat 1.3 Fortsetzung der Studien 1.4 Bibliotheca Hertziana 1.5 Tod 2 Postum 3 ...

Yustinus IIKaisar BizantiumSolidus Yustinus IIBerkuasa15 November 565 – 578PendahuluYustinianus IPenerusTiberius II KonstantinusNama lengkapFlavius Yustinus Junior AugustusAyahDulcidio (atau Dulcissimus)IbuVigilantiaPermaisuriSofiaAnakArabia Yustinus II (bahasa Latin: Flavius Yustinus Junior Augustus; bahasa Yunani: Φλάβιος Ἰουστίνος ὁ νεότερος; skt. 520 – 5 Oktober 578) merupakan seorang Kaisar Romawi Timur (Bizantium) dari tahun 565 hingga 578. Ia adal...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2019) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Hidangan kuil KoreaHidangan kuil Korea di Sanchon, sebuah tempat makan yang terletak di Insadong, Seoul.Nama KoreaHangul사찰음식 Hanja寺刹飮食 Alih Aksarasachal eumsikMcCune–Reischauersach'al ŭmsik Hidangan kuil Korea merujuk kepada jenis hi...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Pretty Wicked – news · newspapers · books · scholar · JSTOR (December 2018) American TV series or program Pretty WickedStarringCariDee EnglishCountry of originUnited StatesNo. of episodes8ProductionRunning time60 minutesOriginal releaseNetworkOxy...

Roman tutelary deity of woods SilvanusTutelary god of woods and uncultivated lands, protector of field boundaries and cattle, protector against wolvesBronze statue of Silvanus, said to be from Nocera in southern Italy.AbodeThe forestSymbolsPan flute, cypressGendermaleEquivalentsGreek equivalentSilenusEtruscan equivalentSelvans? Altar decorated with a bas-relief depicting the god Sylvanus Capitoline Museums in Rome. Silvanus (/sɪlˈveɪnəs/;[1] meaning of the woods in Latin) was a Ro...

Governing body of association football in England This article is about the Football Association of England. For football associations in general, see football association. For more detail on the sport, see association football. The FA redirects here. For other uses, see FA (disambiguation). The Football AssociationUEFAShort nameThe FAFounded26 October 1863; 160 years ago (1863-10-26)HeadquartersWembley StadiumLocationWembley, LondonFIFA affiliation 1905–1920 1924–1928 1...

American animated television series (1986–1991) This article is about the television series. For other uses, see The Real Ghostbusters (disambiguation). The Real GhostbustersTitle cardAlso known asSlimer! and the Real Ghostbusters (seasons 4–7)GenreSupernatural comedy proceduralBased onGhostbustersby Dan Aykroyd Harold RamisDeveloped byJoe MedjuckMichael C. GrossVoices of Lorenzo Music Maurice LaMarche Frank Welker Arsenio Hall Dave Coulier Buster Jones Laura Summer...

Daughter of Husayn ibn Ali This article is about Ruqayya bint al-Husayn. She is not to be confused with Sakinah (Fatima al-Kubra) bint Husayn. Ruqayya bint al-Husaynرُقَيَّة بِنْت ٱلْحُسَيْنBornc. 676 CEMedina, Umayyad CaliphateDiedc. 680 CEDamascus, Umayyad CaliphateResting placeSayyidah Ruqayya Mosque, DamascusParentHusayn ibn Ali (father) Ruqayya bint al-Ḥusayn (Arabic: رُقَيَّة بِنْت ٱلْحُسَيْن) is said to have been a daughter of...

Type of team This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may lack focus or may be about more than one topic. Please help improve this article, possibly by splitting the article and/or by introducing a disambiguation page, or discuss this issue on the talk page. (July 2017) The examples and perspective in this article deal primarily with the United States and do not repres...

David ReedReed in 2008Birth nameDavid Marshall ReedBorn (1982-05-26) 26 May 1982 (age 41)York, EnglandMediumStand up, theatre, radio, televisionNationalityBritishYears active2006–presentGenresSketch comedySpouseDanielle Ward David Reed (born 26 May 1982) is a British actor, writer and comedian and one third of comedy troupe The Penny Dreadfuls.[1] Career Reed studied at the University of Edinburgh. During his studies he performed with the Edinburgh University Theatre Compa...

2018 Indian filmRaakshasTheatrical release posterDirected byDnyanesh ZotingScreenplay byDnyanesh ZotingStory byDnyanesh ZotingTanmayee DeoProduced byNilesh NavalakhaVivek KajariaStarringSharad KelkarSai TamhankarVijay MouryaUmesh JagtapRujuta DeshpandeCinematographyMayur Hardas(Additional Photography)Rakesh BhillareSayak BhattacharyaEdited byMayur Hardas(Co-Editor)Charu Shree RoyMusic byAndrew MackayProductioncompaniesNavalakha Arts and Holy Basil ProductionsDistributed byNavalakha Arts and H...

Illegal activity Part of a series onCannabis ArtsCulture 420 Books Magu (deity) Names Religion Judaism Latter-day Saints Sikhism Smoke-in Spiritual use Sports Stoner film Stoner rock Terms Chemistry Cannabinoid receptors Cannabinoid receptor type 1 Cannabinoid receptor type 2 Cannabinoids 2-AG 2-AGE, Noladin ether AEA CBC CBL CBD CBDV CBG CBN CBV NADA THC THCV Virodhamine Synthetic cannabinoids AM-2201 CP-55940 Dimethylheptylpyran HU-210 HU-331 JWH-018 JWH-073 JWH-133 Levonantradol SR144528 W...

Article connexe : Liste des indicatifs téléphoniques internationaux par pays. Voici la liste des indicatifs téléphoniques internationaux, classés par indicatif, permettant d'utiliser les services téléphoniques vers un autre pays et d'identifier un appel venant d'un pays étranger. Un indicatif téléphonique international est un préfixe téléphonique utilisé dans les numéros de téléphone des pays ou des régions membres de l'Union internationale des télécommunications. L'i...

2017 puzzle video game 2017 video gameDeath SquaredDeveloper(s)SMG StudioPublisher(s)SMG StudioEngineUnityPlatform(s)Microsoft WindowsmacOSNintendo SwitchXbox OnePlayStation 4iOSAndroidAirConsoleRelease March 14, 2017 Microsoft Windows, macOS, PlayStation 4, Xbox One March 14, 2017 Nintendo Switch July 13, 2017 iOS February 13, 2018 Android March 28, 2018 Genre(s)PuzzleMode(s)Cooperative video gamemultiplayersingle-player Death Squared is a puzzle video game developed and published by S...