Teorema Cantor
|
Read other articles:

Jean-Baptiste OlivierPortrait of general Jean-Baptiste OlivierBorn25 December 1765 (1765-12-25)Strasbourg, Haut-Rhin, FranceDied27 September 1813 (1813-09-28) (aged 47)Witternesse, Pas-de-Calais, FranceAllegiance FranceService/branchInfantryYears of service1781–1813RankGeneral of DivisionBattles/warsFrench Revolutionary WarsNapoleonic WarsAwardsLégion d'Honneur, Grand OfficerOrder of the Iron CrownOther workBaron of the Empire Jean-Baptiste Olivier (25 December 1765

СелоБелоречицаукр. Білорічиця 50°40′35″ с. ш. 31°59′50″ в. д.HGЯO Страна Украина Область Черниговская Район Прилукский Сельский совет Белоречицкий История и география Основан 1600 Прежние названия до 1945 — Вейсбаховка Площадь 2,953 км² Высота центра 124 м Тип климата �...

The history of the Baháʼí Faith in Africa dates back to the lifetimes of the three individual heads of the religion, Baháʼu'lláh, ʻAbdu'l-Bahá, and Shoghi Effendi, each of who was in Africa at least once. The Association of Religion Data Archives (relying on World Christian Encyclopedia) lists many larger and smaller populations in Africa[1] with Kenya, the Democratic Republic of the Congo, South Africa and Zambia among the top ten numerical populations of Baháʼís in the wo...

Rheita Foto LRO Kratergegevens Coördinaten 37° 1′ ZB, 47° 2′ OL Diameter 71 km Kraterdiepte 4,3 km Colongitude 314° bij zonsopgang Kaartblad 114 (PDF) Vernoemd naar Anton Maria Schyrleus de Rheita Vernoemd in 1935 Tenzij anders aangegeven, zijn de gegevens ontleend aan de IAU/USGS-Databank Locatie van Rheita samen met Brenner, Metius en Vallis Rheita Rheita is een inslagkrater in het sterk bekraterd zuidoostelijk gebied van de naar de Aarde toegekeerde kant van de Maan. Beschr...

Ne doit pas être confondu avec Île Phanagoria. Cet article est une ébauche concernant la géographie, la Grèce antique et le Haut Moyen Âge. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Phanagoria Localisation Pays Russie Coordonnées 45° 11′ 20″ nord, 36° 49′ 30″ est Géolocalisation sur la carte : Russie européenne PhanagoriaPhanagoria Géolocalisation sur l...

Арфак Країна Індонезія Адміністративна одиниця Західне Папуа Найвища точка Арфакd Висота над рівнем моря 2955 м З матеріалу пісковик, магматичні гірські породи і вапняк Арфак у Вікісховищі Координати: 1°05′ пд. ш. 133°58′ сх. д. / 1.083° пд. ...

واد شديدة تقسيم إداري البلد المغرب الجهة كلميم واد نون الإقليم طانطان الدائرة طانطان الجماعة القروية أبطيح المشيخة النواحي السكان التعداد السكاني 18 نسمة (إحصاء 2004) • عدد الأسر 4 معلومات أخرى التوقيت ت ع م±00:00 (توقيت قياسي)[1]، وت ع م+01:00 (توقيت صيفي)[1] تعدي

تيمزيروليموس الاسم النظامي (1R,2R,4S)-4-{(2R)-2-[(3S,6R,7E,9R,10R,12R,14S,15E,17E,19E,21S,23S,26R,27R,34aS)-9,27-dihydroxy-10,21-dimethoxy-6,8,12,14,20,26-hexamethyl-1,5,11,28,29-pentaoxo-1,4,5,6,9,10,11,12,13,14,21,22,23,24,25,26,27,28,29,31,32,33,34,34a-tetracosahydro-3H-23,27-epoxypyrido[2,1-c] [1,4]oxazacyclohentriacontin-3-yl]propyl}-2-methoxycyclohexyl 3-hydroxy-2-(hydroxymethyl)-2-methylpropanoate يعالج سرطان الكلية، وسرطانة ال

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Scratch or Stitch – news · newspapers · books · scholar · JSTOR (May 2021) (Learn how and when to remove this template message) 1995 studio album by Melt-BananaScratch or StitchStudio album by Melt-BananaReleasedNovember 1995RecordedJuly – August 1995...

Nicolás Suárez Location in Bolivia General Data Capital Cobija Area 9,819 km2 Population 29,536 (2001) Density 3.0 inhabitants/km2 (2001) ISO 3166-2 BO.PA.NS Pando Department Nicolás Suárez is one of the five provinces of the Bolivian Pando department and is situated in the department's northwestern parts. Its name honors Nicolás Suárez Callaú (1861-1940) who owned major parts of today's Pando and Beni Departments in the times of the caoutchouc-boom. Location Nicolás Suárez Prov...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Yoo In-na – berita · surat kabar · buku · cendekiawan · JSTOR Ini adalah nama Korea; marganya adalah Yoo. Yoo In-naYoo In-na pada 2017Lahir5 Juni 1982 (umur 41) Seongnam, Gyeonggi, Korea SelatanPekerjaan...

Space City!Cover of the October 28, 1971, issue. Artwork by Kerry Fitzgerald (Kerry Awn).TypeBiweekly newspaperFormatTabloidOwner(s)Space City News CollectiveEditorFounding Editorial Collective: Thorne Dreyer, Victoria Smith, Sue Mithun Duncan, Cam Duncan, Dennis Fitzgerald, and Judy Gitlin FitzgeraldFounded1969Ceased publication1972HeadquartersHouston, TexasCirculation10,000 Space City! was an underground newspaper published in Houston, Texas from June 5, 1969 to August 3, 1972. The founders...

此條目可参照外語維基百科相應條目来扩充。 (2019年6月13日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 潘興飛彈是當時問世的長程飛彈中較精確一種,掀起冷戰緊張。 1983年優秀射手演習[1](英語:Able Arche...

School district in Union County, New Jersey, United States Roselle Public SchoolsAddress710 Locust Street Roselle, Union County, 07203United StatesCoordinates40°39′07″N 74°15′54″W / 40.651964°N 74.264981°W / 40.651964; -74.264981District informationGradesPreK-12SuperintendentDr. Nathan L. FisherBusiness administratorAnthony JuskiewiczSchools8Students and staffEnrollment2,897 (as of 2020–21)[1]Faculty289.0 FTEs[1]Student–teacher ratio10.0...
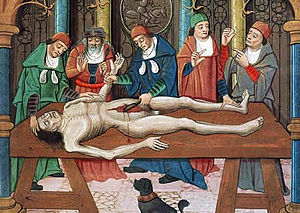
Aspect of history Dissection of a cadaver, 15th-century painting The history of anatomy extends from the earliest examinations of sacrificial victims to the sophisticated analyses of the body performed by modern anatomists and scientists. Written descriptions of human organs and parts can be traced back thousands of years to ancient Egyptian papyri, where attention to the body was necessitated by their highly elaborate burial practices. Theoretical considerations of the structure and function...

Noureddine Naybet Informasi pribadiNama lengkap Noureddine NaybetTanggal lahir 10 Februari 1970 (umur 53)Tempat lahir Casablanca, MoroccoTinggi 183 m (600 ft)Posisi bermain Centre backKarier senior*Tahun Tim Tampil (Gol)1989–1993 WAC 75 (4)1993–1994 Nantes 34 (1)1994–1996 Sporting CP 54 (5)1996–2004 Deportivo La Coruña 211 (11)2004–2006 Tottenham Hotspur 30 (1)Total 404 (22)Tim nasional1990–2006 Morocco 115 (4) * Penampilan dan gol di klub senior hanya dihitung dar...

Gaya atau nada penulisan artikel ini tidak mengikuti gaya dan nada penulisan ensiklopedis yang diberlakukan di Wikipedia. Bantulah memperbaikinya berdasarkan panduan penulisan artikel. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Swami Anand KrishnaLahir1 September 1956 (umur 67)SurakartaSuami/istriRani Gangtani (menikah 26 Oktober 1977)[1]AnakPooja Gangtani (anak laki-laki)Prashant Gangtani (anak laki-laki)[1]Orang tuaTolaram (ayah)[2]Situs...

Finnish-American actress and television personality Maila NurmiNurmi in 1947BornMaila Elizabeth Syrjäniemi(1922-12-11)December 11, 1922Gloucester, Massachusetts, U.S.[a]DiedJanuary 10, 2008(2008-01-10) (aged 85)Los Angeles, California, U.S.Resting placeHollywood Forever CemeteryOther namesMaila Niemi NurmiMaila Elizabeth NurmimioniVampiraOccupationActressSpouses Dean Riesner (m. 1949) John Brinkley (m. 1958) Fabr...

Species of fungus Morchella pragensis Scientific classification Domain: Eukaryota Kingdom: Fungi Division: Ascomycota Class: Pezizomycetes Order: Pezizales Family: Morchellaceae Genus: Morchella Species: M. pragensis Binomial name Morchella pragensisSmotl. (1952) Synonyms[1] Morchella pterigoides Smotl. & M.Kolařík Morchella pragensis f. mirabilis Smotl. (1952) Morchella pragensis f. turriformis Smotl. (1952) Morchella pragensis f. pterigoides (Smotl. & M.Kolařík) J.V...

2001 film by Sundar C. Ullam Kollai PoguthaeDirected bySundar C.Written byA. C. Mugil (dialogues)Screenplay bySundar C.Story byA. C. MugilProduced byK. MuralitharanV. SwaminathanG. VenugopalStarringPrabhu DevaAnjala ZaveriCinematographyU. K. Senthil KumarEdited byP. Sai SureshMusic byKarthik RajaProductioncompanyLakshmi Movie MakersDistributed byLakshmi Movie MakersRelease date 9 February 2001 (2001-02-09) Running time143 minutesCountryIndiaLanguageTamil Ullam Kollai Poguthae i...
































































