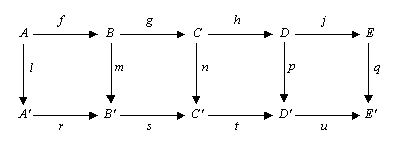
Aljabar homologis
|
Read other articles:

Ruinen des Asklepieions von Kos Das Asklepieion von Kos ist die bedeutendste archГӨologische StГӨtte auf der Insel Kos. Das antike Heiligtum des Asklepios (Asklepieion) liegt knapp 4 km in sГјdwestlicher Richtung, auГҹerhalb der heutigen Inselhauptstadt auf einem von Zypressen bewaldeten HГјgel, knapp 100 m Гјber dem Meeresspiegel. Es wurde 1901 nach Hinweisen des von Kos stammenden Historikers Iakovos Zaraftis von dem deutschen ArchГӨologen Rudolf Herzog entdeckt und freigelegt. Die Aus...

СҒРөР»Рҫ РӣСғРІРөРҪСҢРіР° РӣСғРІРөРҪСҢРіР° РҡСҖаїРҪР° Р РҫСҒС–СҸ РЎСғРұ'С”РәСӮ Р РҫСҒС–Р№СҒСҢРәРҫС— РӨРөРҙРөСҖР°СҶС–С— РңСғСҖРјР°РҪСҒСҢРәР° РҫРұлаСҒСӮСҢ РңСғРҪС–СҶРёРҝалСҢРҪРёР№ СҖайРҫРҪ РҡР°РҪРҙалаРәСҒСҢРәРёР№ СҖайРҫРҪ РҹРҫСҒРөР»РөРҪРҪСҸ РҡР°РҪРҙалаРәСҒСҢРәРө РјС–СҒСҢРәРө РҝРҫСҒРөР»РөРҪРҪСҸ РҡРҫРҙ Р—РҡРҗРўРЈ: 47202000015 РҡРҫРҙ Р—РҡРўРңРһ: 47608101106 РһСҒРҪРҫРІРҪС– РҙР°РҪС– РқР°СҒРөР»РөРҪРҪСҸ в–ј 575 РҹРҫСҲСӮРҫРІРёР№ С–РҪРҙРөРәСҒ 184015 РўРөР»РөС„РҫРҪРҪРёР№ РәРҫРҙ +7&#...

ЩҮШ°ЩҮ Ш§Щ„Щ…ЩӮШ§Щ„Ш© ЩҠШӘЩҠЩ…Ш© ШҘШ° ШӘШөЩ„ ШҘЩ„ЩҠЩҮШ§ Щ…ЩӮШ§Щ„Ш§ШӘ ШЈШ®ШұЩү ЩӮЩ„ЩҠЩ„Ш© Ш¬ШҜЩӢШ§. ЩҒШ¶Щ„ЩӢШ§ШҢ ШіШ§Ш№ШҜ ШЁШҘШ¶Ш§ЩҒШ© ЩҲШөЩ„Ш© ШҘЩ„ЩҠЩҮШ§ ЩҒЩҠ Щ…ЩӮШ§Щ„Ш§ШӘ Щ…ШӘШ№Щ„ЩӮШ© ШЁЩҮШ§. (ШіШЁШӘЩ…ШЁШұ 2019) Ш§Ш¶ШәШ· ЩҮЩҶШ§ Щ„Щ„Ш§Ш·Щ„Ш§Ш№ Ш№Щ„Щү ЩғЩҠЩҒЩҠШ© ЩӮШұШ§ШЎШ© Ш§Щ„ШӘШөЩҶЩҠЩҒ Ш§Щ„Ш¬ШұШ§ШҜ Ш§Щ„Щ…ЩҮШ§Ш¬Шұ ШөЩҲШӘ Ш§Щ„Ш¬ШұШ§ШҜ Ш§Щ„Щ…ЩҮШ§Ш¬Шұ noicon Ш§Щ„Щ…ШұШӘШЁШ© Ш§Щ„ШӘШөЩҶЩҠЩҒЩҠШ© ЩҶЩҲШ№ Ш§Щ„ШӘШөЩҶЩҠЩҒ Ш§Щ„Ш№Щ„Щ…ЩҠ ЩҒЩҲЩӮ Ш§Щ„ЩҶШ·Ш§ЩӮ ШӯЩҠЩҲЩҠШ§ШӘ Щ…Щ…Щ„ЩғШ© Ш...

2019 Indian general election in Puducherry ← 2014 April 18, 2019 (2nd phase) 1 seatTurnout81.20 First party Second party Leader Rahul Gandhi N. Rangaswamy Party INC AINRC Alliance UPA NDA Last election 0 1 Seats won 1 0 Seat change 1 1 Popular vote 4,44,981 2,47,956 Percentage 56.27% 31.36% Swing 29.92% 3.21% The 2019 Indian general elections was held in seven phases from 11 April to 19 May 2019 to constitute the 17th Lok Sabha. The general electio...

Delegation of the European Union to the United KingdomLocationWestminster, LondonAddress32 Smith Square, London, SW1P 3EUCoordinates51В°29вҖІ44.3вҖіN 0В°7вҖІ39.4вҖіW / 51.495639В°N 0.127611В°W / 51.495639; -0.127611AmbassadorJoГЈo Vale de AlmeidaPart of a series of articles onUK membershipof the European Union(1973вҖ“2020) Accession Treaty of Accession 1972 1972 EC Act 1973 enlargement of the EC 1975 referendum Referendum Act (results) Treaty amendments Single European...

Species of gastropod Liotella kilcundae Original drawing with three views of a shell of Liotella kilcundai Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Mollusca Class: Gastropoda Subclass: Vetigastropoda Order: Trochida Superfamily: Trochoidea Family: Skeneidae Genus: Liotella Species: L. kilcundae Binomial name Liotella kilcundae(Gatliff & Gabriel, 1914) Synonyms Chunula kilcundae (Gatliff & Gabriel, 1914) Cyclostrema kilcundae Gatliff & Gabriel, 191...

District of Liberia This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: District 2, Grand Bassa County вҖ“ news В· newspapers В· books В· scholar В· JSTOR (December 2009) (Learn how and when to remove this template message) Location of District #2 in Grand Bassa County District #2 is one of six districts located in Grand Bassa County, ...

River in Yakutia, Russia For the river of the Alazeya basin, see Arga-Yuryakh (Rassokha). Arga-YuryakhРҗСҖРіР°-Р®СҖСҸС… / РҗСҖҕаа Т®СҖСҚС…Last stretch of the Arga-Yuryakh Sentinel-2 imageMouth location in Yakutia, RussiaLocationCountryRussiaPhysical characteristicsSource • locationOrulgan RangeVerkhoyansk Range • coordinates69В°49вҖІ31вҖіN 130В°20вҖІ48вҖіE / 69.82528В°N 130.34667В°E / 69.82528; 130.34667 • e...

Fictional street address in Springfield of the Simpson family home 742 Evergreen TerraceThe Simpsons locationThe exterior, as seen in the episode Beyond Blunderdome (1999).First appearanceGood Night (1987)Created byMatt GroeningIn-universe informationOther name(s)The Simpsons houseTypeResidential houseLocationSpringfield, United StatesCharactersHomer SimpsonMarge SimpsonBart SimpsonLisa SimpsonMaggie SimpsonSanta's Little HelperSnowball II The Simpsons house is the residence of the Simpson fa...

Portuguese cycling team W52вҖ“FC PortoTeam informationUCI codeW52RegisteredPortugalFounded2004 (2004)Disbanded2022Discipline(s)RoadStatusAmateur (2004вҖ“2012)UCI Continental (2013вҖ“2018, 2020вҖ“2022)UCI Professional Continental (2019)BicyclesSwiftCarbonWebsiteTeam home pageKey personnelGeneral managerAdriano SousaTeam manager(s)Nuno RibeiroHГ©lder AlvesTeam name history2004вҖ“20052006вҖ“200720082009вҖ“2010201120122013вҖ“20142015201620172018вҖ“2022CasactivaвҖ“Quinta das ArcasвҖ“UCSCasact...

Comics character The WrathCover of Batman Special #1 (June 1984).Publication informationPublisherDC ComicsFirst appearance(Wrath I)Batman Special #1(June 1984)(Wrath II)Batman Confidential #13 (March 2008)Created by(Wrath I)Mike W. Barr (writer)Michael Golden (artist) (Wrath II)Tony Bedard (writer)Rags Morales (artist)In-story informationAlter ego(Wrath I) Unknown (Wrath II) Elliot CaldwellSpeciesHuman The Wrath is the name of two fictional supervillains published by DC Comics. The original W...

American western drama television series The SonGenre Western Drama Based onThe Sonby Philipp MeyerDeveloped by Philipp Meyer Lee Shipman Brian McGreevy Starring Pierce Brosnan Henry Garrett Zahn McClarnon Jess Weixler Paola NГәГұez Elizabeth Frances Sydney Lucas Jacob Lofland David Wilson Barnes James Parks Shane Graham Kathryn Prescott Sean Alan Stone ComposerNathan BarrCountry of originUnited StatesOriginal languageEnglishNo. of seasons2No. of episodes20 (list of episodes)ProductionExecuti...

2006 studio album by Radio 4Enemies Like ThisStudio album by Radio 4ReleasedMay 16, 2006RecordedNew York City, 2006GenreDance-punk, post-punk revivalLength41:43LabelAstralwerks RecordsRadio 4 chronology Stealing of a Nation(2004) Enemies Like This(2006) Singles from Enemies Like This Enemies Like ThisReleased: May 2006 Packing Things up on the SceneReleased: October 2006 As Far As the Eye Can SeeReleased: 2006 / 2007 Enemies Like This is the fourth LP by the New York City dance-punk b...

Comic book superhero This article is about the Marvel Comics character. For the martial arts film, see Ironheart (1992 film). For the television series, see Ironheart (miniseries). For other uses, see Iron Heart (disambiguation). Comics character IronheartRiri Williams on the cover ofIronheart #1 (2020)Art by S Skan.Publication informationPublisherMarvel ComicsFirst appearanceCameo appearance:Invincible Iron Man Vol. 2 #7 (May 2016)Full appearance:Invincible Iron Man Vol. 2 #9 (July 2016)As I...

Pakistani cricketer PP SIMisbah-ul-HaqMisbah-ul-HaqPersonal informationFull nameMisbah-ul-HaqBorn (1974-05-28) 28 May 1974 (age 49)Mianwali, Punjab, PakistanNicknameMan of Crisis[1][2][3]Height6 ft 1 in (185 cm)[4]BattingRight-handedBowlingRight-arm leg breakRoleBatsmanInternational information National sidePakistan (2001вҖ“2017)Test debut (cap 166)8 March 2001 v New ZealandLast Test14 May 2017 v West Indies...
ЩғЩҲШұШӘ ШЁШұЩҠЩҶШІЩ„ШҢ Щ…Щ„Ш§ЩғЩ… Щ…ЩҶ Ш№ШҙШұЩҠЩҶЩҠШ§ШӘ Ш§Щ„ЩӮШұЩҶ Ш§Щ„Щ…Ш§Ш¶ЩҠШҢ ЩҠШёЩҮШұ Ш§Щ„Щ…ЩҲЩӮЩҒ Ш§Щ„ШЈШұШ«ЩҲШ°ЩғШіЩҠ ШЁЩҠШҜЩҮ Ш§Щ„ЩҠШіШұЩү ЩҲШ§Щ„ЩӮШҜЩ… Ш§Щ„ЩҠШіШұЩү ЩҒЩҠ Ш§Щ„Щ…ЩӮШҜЩ…Ш© ЩҒЩҠ Ш§Щ„ШұЩҠШ§Ш¶Ш§ШӘ Ш§Щ„ЩӮШӘШ§Щ„ЩҠШ© Щ…Ш«Щ„ Ш§Щ„Щ…Щ„Ш§ЩғЩ…Ш©ШҢ ЩҲЩӮЩҒШ© Ш§Щ„ШЈШұШ«ЩҲШ°ЩғШіЩҠ (ШЁШ§Щ„ШҘЩҶШ¬Щ„ЩҠШІЩҠШ©: Orthodox stance)вҖҸ ЩҮЩҲ Ш§Щ„Щ…ЩҲЩӮЩҒ Ш§Щ„Ш°ЩҠ ЩҠШ¶Ш№ ЩҒЩҠЩҮ Ш§Щ„Щ…Щ„Ш§ЩғЩ… ЩӮШҜЩ…ЩҮ Ш§Щ„ЩҠШіШұЩү ШЁШ№ЩҠШҜЩӢШ§ ШЈЩ…Ш§Щ… Ш§Щ„ЩӮШҜЩ… Ш§Щ„ЩҠЩ…ЩҶЩүШҢ ЩҲШЁШ§Щ„ШӘШ§Щ„ЩҠ ЩҠЩғЩҲЩҶ Ш¬Ш§ЩҶШЁЩҮ ...

Albanian Coast Guard class Iliria-class patrol vessel Iliria-class patrol vessel of the Albanian Coast Guard Class overview NameIliria-class BuildersDamen Group; Pashaliman Shipyard OperatorsAlbanian Coast Guard Built2007вҖ“2014 In service2008вҖ“Present In commission2008вҖ“2014 Completed4 Active4 General characteristics TypePatrol vessel Displacement208 t (205 long tons; 229 short tons) Length42.8 m (140 ft) Beam7.11 m (23.3 ft) Draft2.5 m (8 ft 2 in) D...

Qaasuitsup KommuniaMunisipalitas di Greenland2009вҖ“2017 Coat of arms Lokasi Qaasuitsup di GreenlandIbu kotaIlulissatLuas вҖў Coordinates69В°13вҖІN 51В°06вҖІW / 69.217В°N 51.100В°W / 69.217; -51.100 вҖў 2015660.000 km2 (250.000 sq mi)Populasi вҖў 2015 17168 SejarahSejarah вҖў Didirikan 1 Januari 2009вҖў Dibubarkan 31 Desember 2017 Didahului oleh Digantikan oleh Aasiaat Kangaatsiaq Ilulissat Qaanaaq Qasigianng...

Festival de Cine de AlcalГЎ de Henares Cartel anunciador de ALCINE en la calle Mayor.Datos bГЎsicosNombre oficial Festival de Cine de AlcalГЎ de Henares / Comunidad de MadridOtros nombres ALCINETipo CortometrajeSede Oficina de Eventos, ConcejalГӯa de Cultura c/ San Juan s/nUbicaciГіn AlcalГЎ de HenaresComunidad de Madrid Comunidad de MadridEspaГұa EspaГұaPrimera ediciГіn 1970Organizador Ayuntamiento de AlcalГЎ de HenaresComunidad de MadridGalardГіn Ciudad de AlcalГЎIdioma Espa...

ШіЩҶЩҲШіШұШӘ Ш§Щ„ШЈЩҲЩ„Ш®ШЁШұ ЩғШ§ ШұШ№ШӘЩ…Ш«Ш§Щ„ Щ„ШіЩҶЩҲШіШұШӘ Ш§Щ„ШЈЩҲЩ„ Ш§Щ„Щ…ШӘШӯЩҒ Ш§Щ„Щ…ШөШұЩҠ ШЁШ§Щ„ЩӮШ§ЩҮШұШ©ЩҒШұШ№ЩҲЩҶ Щ…ШөШұШ§Щ„ШӯЩӮШЁШ©1971вҖ“1926 ЩӮ.Щ…, Ш§Щ„ШЈШіШұШ© Ш§Щ„Ш«Ш§ЩҶЩҠШ© Ш№ШҙШұШіШЁЩӮЩҮШЈЩ…ЩҶЩ…ШӯШ§ШӘ Ш§Щ„ШЈЩҲЩ„ШӘШЁШ№ЩҮШЈЩ…ЩҶЩ…ШӯШ§ШӘ Ш§Щ„Ш«Ш§ЩҶЩҠ Ш§Щ„ШЈЩ„ЩӮШ§ШЁ Ш§Щ„Щ…Щ„ЩғЩҠШ© Ш§ШіЩ… Ш§Щ„ШӘШӘЩҲЩҠШ¬: Ш®ЩҫШұ ЩғШ§ ШұШ№ Щ„ЩӮШҜ Ш®ЩҸЩ„ЩӮШӘ ШұЩҲШӯ ШұШ№ Ш§Щ„Ш§ШіЩ… Ш§Щ„ШҙШ®ШөЩҠ: ШіЩҶ ЩҲШіШұШӘ ШұШ¬Щ„ ЩҲШіШұШӘ Ш§ШіЩ… ШӯЩҲШұШі: Ш№ЩҶШ® Щ…ШіЩҲШӘ ШӯЩҠ Ш§Щ„ЩҲЩ„Ш§ШҜШ...